Kalkulator Trygonometrii
Łatwe obliczanie wartości trygonometrycznych Sin, Cos, Tan, Cot, Sec i Csc za pomocą naszego bezpłatnego kalkulatora online!
Spis treści
| ◦Czym jest trygonometria? |
| ◦Jakie są podstawowe lub podstawowe funkcje trygonometryczne? |
| ◦Czym są odwrotne funkcje trygonometryczne? |
| ◦Do czego służy trygonometria? |
| ◦Rzeczywiste zastosowania trygonometrii |
Czym jest trygonometria?
Jakie są podstawowe lub podstawowe funkcje trygonometryczne?
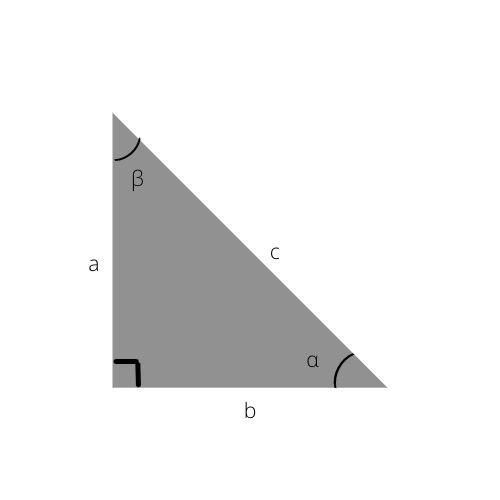
1) Sinus kąta
2) Cosinus kąta
3) Styczna do kąta
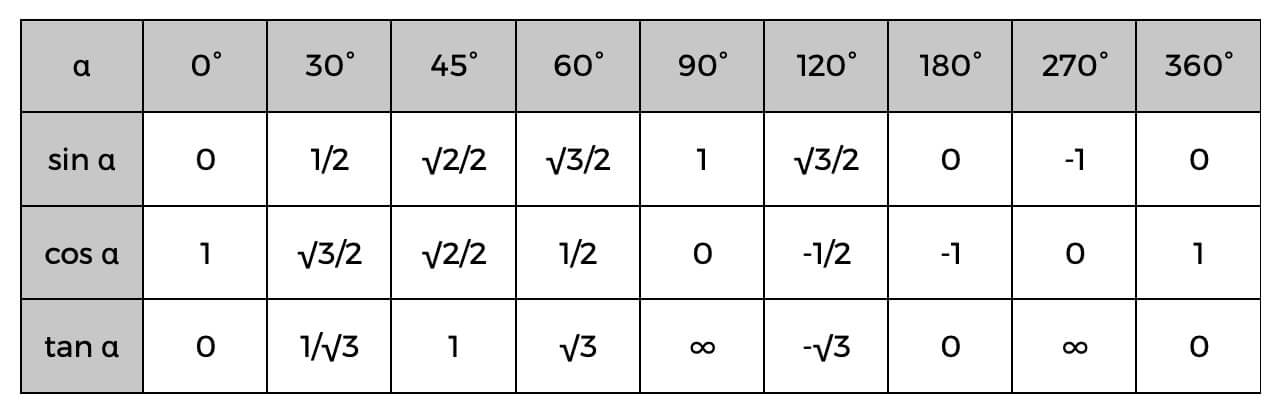
Czym są odwrotne funkcje trygonometryczne?
Do czego służy trygonometria?
Rzeczywiste zastosowania trygonometrii
1) Architektura i inżynieria

2) Astronomia
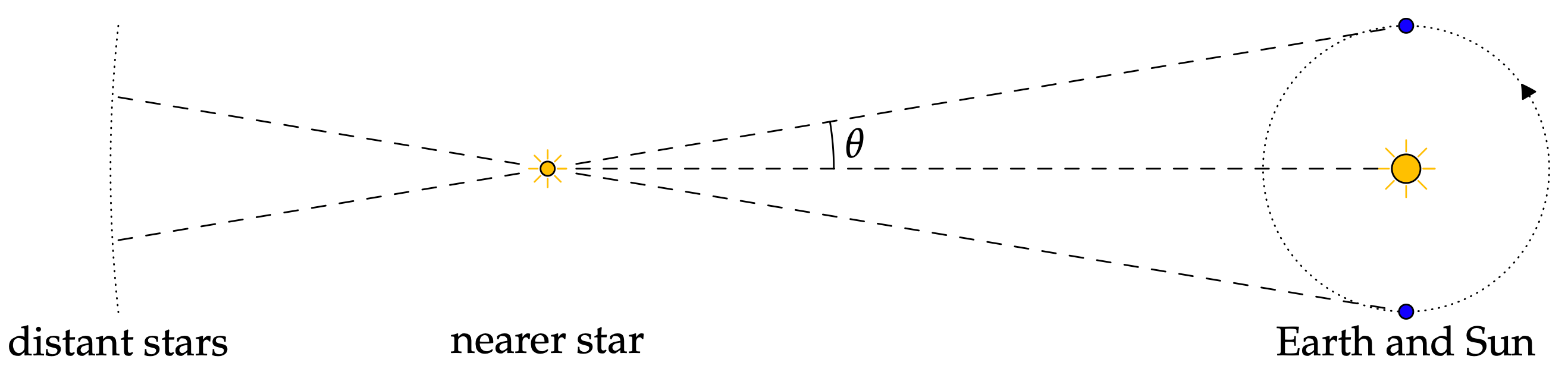
3) Elektronika i elektrotechnika
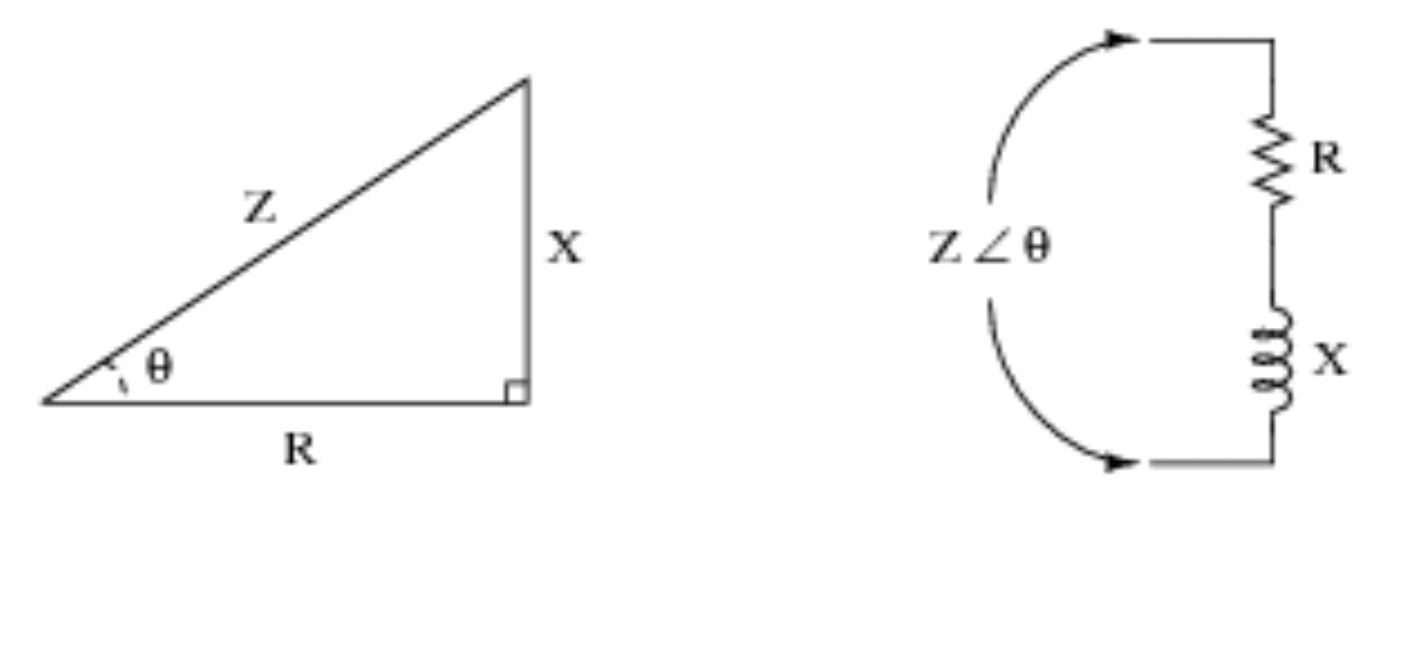
4) Sejsmologia

5) Geodezja (inżynieria lądowa)


Kalkulator Trygonometrii Polski
Inne kalkulatory matematyczne
Kalkulator iloczynu krzyżowego wektorów znajduje iloczyn krzyżowy dwóch wektorów w przestrzeni trójwymiarowej.
Za pomocą naszego kalkulatora trójkątów 30 60 90 możesz rozwiązać specjalny trójkąt prostokątny.
Ten kalkulator wartości oczekiwanej pomaga obliczyć wartość oczekiwaną (zwaną również średnią) danego zestawu zmiennych wraz z ich prawdopodobieństwami.
Ten kalkulator naukowy zapewnia proste i zaawansowane funkcje matematyczne w łatwej w użyciu aplikacji.
Ten darmowy kalkulator podaje odchylenie standardowe, wariancję, średnią i sumę danego zestawu danych.
Ten kalkulator procentowy to darmowy kalkulator online do obliczania procentów. Dowiedz się, co to jest X % Y?
Ten darmowy kalkulator ułamków może służyć do znajdowania wyników dodawania, odejmowania, mnożenia i dzielenia dwóch wspólnych ułamków.
Znajdź prawidłowe wymiary swojego ulubionego przepisu za pomocą tego bezpłatnego kalkulatora, który z łatwością przelicza funty na kubki! Współpracuje z kubkami US i kubkami UK!
Użyj tego bezpłatnego kalkulatora obwodu koła, aby obliczyć promień okręgu, średnicę okręgu, obwód okręgu i obszar okręgu.
Wyznacz ekwiwalent podwójnego kąta dla danego kąta za pomocą tego darmowego kalkulatora! Znajdź więcej informacji o formule podwójnego kąta.
Ten darmowy kalkulator oblicza drugi, trzeci i wyższe wykładniki oraz pierwiastki. Dostępna jest również formuła.
Znajdź obszar trójkąta łatwo za pomocą naszego bezpłatnego kalkulatora obszaru trójkąta! Możesz obliczyć z podstawą i wysokością, trzema różnymi stronami i wieloma innymi. Działa z kątami i radianami!
Znajdź kąty coterminal za pomocą naszego kalkulatora kąta coterminal! Współpracuje ze stopniami i radianami, aby znaleźć dodatnie i ujemne kąty koterminalne!
Łatwo obliczaj matematyczne iloczyny skalarne, iloczyny skalarne i kąty iloczynów skalarnych dla swoich wektorów.
Znajdź łatwo punkty środkowe linii lub trójkąta za pomocą naszego kalkulatora punktów środkowych! Ta strona nauczy Cię również wartościowej formuły punktu środkowego!
Łatwo znajdź prawidłową liczbę cyfr znaczących w swojej liczbie dzięki naszemu narzędziu do cyfr znaczących!
Dowiedz się z łatwością długości łuku koła za pomocą kalkulatora matematycznego online!
Łatwo oblicz oszacowanie punktów za pomocą naszego bezpłatnego narzędzia online!
Łatwo oblicz procentowy wzrost dzięki naszemu bezpłatnemu kalkulatorowi online!
Oblicz różnicę procentową natychmiast za pomocą naszego matematycznego kalkulatora różnic procentowych!
Ten darmowy kalkulator online oblicza interpolację liniową i ekstrapolację liniową. Zapewnia również nachylenie równania liniowego.
Znajdź łatwo macierze ortonormalne i macierze górnego trójkąta za pomocą naszego bezpłatnego internetowego kalkulatora rozkładu QR!
Ten kalkulator transpozycji macierzy pomaga znaleźć transpozycję dla dowolnej macierzy.
Dowiedz się z łatwością przeciwprostokątnej dla wszystkich rodzajów trójkątów dzięki naszemu bezpłatnemu kalkulatorowi matematycznemu!
Dowiedz się z łatwością prawą stronę i kąt trójkąta za pomocą naszego bezpłatnego kalkulatora online!
Oblicz przeciwprostokątną, pomiary i proporcje z łatwością za pomocą naszego kalkulatora trójkątów 45 45 90.
Łatwe obliczanie mnożenia macierzy za pomocą naszego bezpłatnego kalkulatora matematycznego online!
Łatwo oblicz średnią liczb za pomocą naszego bezpłatnego kalkulatora matematycznego online
To narzędzie generuje naprawdę losową liczbę między dowolnymi dwiema liczbami.
Ten kalkulator oblicza margines błędu dla ankiet na podstawie wielkości próby i proporcji. Pozwala również ustawić pożądany poziom pewności siebie.
To narzędzie online oblicza kąt między dwoma wektorami i posiada wszystkie możliwe kombinacje wektorów.
Ten kalkulator pomoże Ci znaleźć LCM lub LCD dla określonego zestawu liczb.
Ten kalkulator online oblicza powierzchnię kształtu mierzoną w stopach. Działa ze wszystkimi kształtami i jednostkami miary!
Jest to kalkulator online, który może obliczyć wykładniki.
To narzędzie online oblicza pozostałą część dywizji.
Z łatwością obliczaj bezpośrednie proporcje liczb za pomocą naszego bezpłatnego kalkulatora Reguła Trzech.
Równania kwadratowe są dowolną algebrą wielomianową drugiego stopnia o następującej postaci w algebrze.
Ten kalkulator notacji sumarycznej pozwala szybko obliczyć sumę ustawionej liczby, znanej również jako Sigma. Dlatego jest często nazywany kalkulatorem sigma. Daje również próbkę z serii, która ma być sumą. Może być używany w trybie prostym do obliczenia prostej sumy przy użyciu danego zestawu liczb.
Jest to bezpłatne narzędzie online, które obliczy obwód różnych kształtów.
Jest to kalkulator, który oblicza wskaźnik Z zestawu danych.
Ten kalkulator Fibonacciego może być używany do dowolnego obliczania warunków ciągu Fibonacciego.
Jest to darmowy kalkulator, który pomoże Ci znaleźć objętość każdej kapsułki.
Jest to darmowy kalkulator, który pomoże Ci znaleźć objętość o różnych kształtach.
Jest to darmowy kalkulator, który pomoże Ci znaleźć objętość dowolnego trójkątnego pryzmatu.
Jest to darmowy kalkulator, który pomoże Ci określić objętość pudełka.
Ten kalkulator oblicza objętość szyszki i może być używany do rozwiązywania problemów szkolnych.
Jest to narzędzie online, które obliczy objętość dowolnej kostki.
Jest to narzędzie online, które obliczy objętość cylindra.
Jest to kalkulator online, który pomoże Ci obliczyć dylatację współczynnika skali obiektu.
Kalkulator indeksu bioróżnorodności Shannona może służyć do obliczania różnorodności gatunków w społeczności. Ekolodzy mogą korzystać ze wskaźnika różnorodności Shannona, aby uzyskać przydatne informacje o siedlisku.
Użyj tego kalkulatora twierdzenia Bayesa online, aby określić prawdopodobieństwo zdarzenia, które jest uzależnione od innego. Obliczenie to uwzględnia prawdopodobieństwo a priori A, prawdopodobieństwa warunkowe B i warunkowe A oraz warunkowe A.
Kalkulator antylogowy pozwala obliczyć funkcję odwrotnego logarytmu. Oblicz antylogarytm dla dowolnej liczby o dowolnej podstawie, niezależnie od tego, czy jest to 10, antylog naturalny, czy inna liczba.
To niesamowite narzędzie pozwoli Ci obliczyć e do potęgi dowolnej wybranej liczby.
Ten kalkulator pokaże Ci, czy liczba ma liczbę pierwszą, czy jest złożoną.
Wykładniczy Kalkulator Wzrostu oblicza ostateczną cenę ilości na podstawie jej wartości początkowych, tempa wzrostu i czasu.
Oblicz wielkość próby na podstawie wielkości populacji, poziomu ufności i marginesu błędu.
Ten kalkulator online wyświetli logarytm odwrotny liczby i wprowadzonej podstawy.
Kalkulator rozkładu Poissona pozwoli Ci określić prawdopodobieństwo wystąpienia zdarzenia kilka razy w określonym przedziale czasowym.
Ten kalkulator pomoże Ci znaleźć odwrotność multiplikatywną liczby całkowitej, ułamka dziesiętnego, ułamka lub liczby mieszanej.
Ten kalkulator zamienia oceny egzaminacyjne na wartości procentowe. Można go wykorzystać do szybkiego obliczenia procentu jednej lub więcej ocen z testu (ocen) oraz maksymalnej liczby ocen.
Ten kalkulator może służyć do określania wymiarów obrazów podczas ich zmiany rozmiaru.
Kalkulator reguł empirycznych, znany również jako „obliczanie reguł 68 95 99”, to narzędzie, które pozwala określić zakresy, które są 1 lub 2 odchyleniami standardowymi lub 3 odchyleniami standardowymi. Ten kalkulator pokaże zakresy, w których odpowiednio 68, 95 lub 99,7% danych o rozkładzie normalnym.
To niesamowite narzędzie pozwoli Ci znaleźć wartość p. Możesz użyć statystyk testowych, aby określić, która wartość p jest jednostronna, a która dwustronna.
Jest to darmowy kalkulator, który pomoże Ci znaleźć objętość kuli.
Ten kalkulator online pozwoli Ci obliczyć NPV (obecną wartość netto) inwestycji. Kalkulacja oparta jest na początkowej inwestycji i stopie dyskontowej. Możesz także obliczyć wewnętrzne stopy zwrotu (IRR), zwroty brutto i przepływy pieniężne netto.
Użyj tego kalkulatora, aby dowiedzieć się, jak procentowy spadek o dowolną kwotę zmieni wynik. Wystarczy wprowadzić pierwotną wartość, procentowy spadek i nową wartość, aby obliczyć zmianę.
Nasze intuicyjne narzędzie pozwala wybierać spośród różnych kształtów i oblicza ich powierzchnię w mgnieniu oka.
Kalkulator prawdopodobieństwa umożliwia zbadanie relacji prawdopodobieństwa między dwoma oddzielnymi zdarzeniami. Pozwala to lepiej zrozumieć, w jaki sposób zdarzenia są ze sobą powiązane, a tym samym sprawia, że prognozy są dokładniejsze.
Skorzystaj z naszego kalkulatora ułamków zwykłych na dziesiętne, aby łatwo przekonwertować ułamki zwykłe na dziesiętne iz powrotem!
Znajdź czynniki dowolnej liczby za pomocą naszego kalkulatora współczynników
Zamień ułamek na kalkulator liczb mieszanych za pomocą naszego prostego narzędzia