30 60 90 Dreiecksrechner
Mit unserem 30 60 90 Dreiecksrechner können Sie das spezielle rechtwinklige Dreieck lösen.
Inhaltsverzeichnis
Was ist ein 30 60 90 Dreieck?
30-60-90 ist eine besondere Art von Dreieck
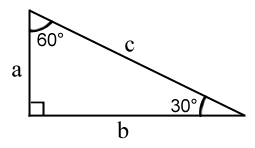
Welche Seite des Dreiecks 30 60 90 ist welche?
Dreieck berechnen, a finden, b finden
Wie löst man das spezielle rechtwinklige Dreieck?
Spezielles rechtwinkliges Dreiecksverhältnis

30 60 90 Dreiecksrechner Deutsch
Andere mathematische Taschenrechner
Der Vektor-Kreuzproduktrechner ermittelt das Kreuzprodukt zweier Vektoren in einem dreidimensionalen Raum.
Dieser Erwartungswertrechner hilft Ihnen, einen Erwartungswert (auch Mittelwert genannt) der gegebenen Variablenmenge mit ihren Wahrscheinlichkeiten zu berechnen.
Dieser wissenschaftliche Taschenrechner bietet einfache und erweiterte mathematische Funktionen in einer benutzerfreundlichen App.
Dieser kostenlose Rechner gibt Ihnen die Standardabweichung, Varianz, Mittelwert und Summe eines bestimmten Datensatzes.
Dieser Prozentrechner ist ein kostenloser Online-Rechner zur Berechnung von Prozentsätzen. Finden Sie heraus, was X % von Y ist?
Dieser kostenlose Bruchrechner kann verwendet werden, um das Ergebnis zum Addieren, Subtrahieren, Multiplizieren und Dividieren von zwei gemeinsamen Brüchen zu finden.
Finden Sie mit diesem kostenlosen Rechner die korrekten Maße für Ihr Lieblingsrezept heraus und wandeln Sie ganz einfach Pfund in Tassen um! Funktioniert mit US-Cups und UK-Cups!
Verwenden Sie diesen kostenlosen Kreisumfangsrechner, um Kreisradius, Kreisdurchmesser, Kreisumfang und Kreisfläche zu berechnen.
Bestimmen Sie das doppelte Winkeläquivalent eines gegebenen Winkels mit diesem kostenlosen Rechner! Weitere Informationen zur Doppelwinkelformel.
Dieser kostenlose Rechner berechnet den zweiten, dritten und höheren Exponenten und Wurzeln. Formel ist auch verfügbar.
Finden Sie die Fläche des Dreiecks ganz einfach mit unserem kostenlosen Dreiecksflächenrechner heraus! Sie können mit Basis und Höhe, drei verschiedenen Seiten und vielem mehr rechnen. Funktioniert mit Winkeln und Bogenmaß!
Finden Sie coterminale Winkel mit unserem coterminalen Winkelrechner heraus! Funktioniert mit Grad und Bogenmaß, um positive und negative coterminale Winkel zu ermitteln!
Berechnen Sie einfach mathematische Punktprodukte, Skalarprodukte und Punktproduktwinkel für Ihre Vektoren.
Mit unserem Mittelpunktrechner ermitteln Sie ganz einfach Mittelpunkte einer Linie oder eines Dreiecks! Diese Seite wird Ihnen auch wertvolle Mittelpunktformel beibringen!
Finden Sie mit unserem Signifikanz-Tool ganz einfach die richtige Anzahl signifikanter Zahlen in Ihrer Zahl heraus!
Finden Sie mit diesem Online-Mathe-Rechner ganz einfach die Länge eines Kreisbogens heraus!
Berechnen Sie die Punktschätzung ganz einfach mit unserem kostenlosen Online-Tool!
Berechnen Sie jede prozentuale Erhöhung ganz einfach mit unserem kostenlosen Online-Rechner!
Berechnen Sie die prozentuale Differenz sofort mit unserem mathematischen prozentualen Differenzrechner!
Dieser kostenlose Online-Rechner berechnet die lineare Interpolation und die lineare Extrapolation. Es liefert auch die Steigung der linearen Gleichung.
Finden Sie die Orthonormalmatrix und die obere Dreiecksmatrix ganz einfach mit unserem kostenlosen Online-QR-Zerlegungsrechner heraus!
Dieser Matrixtransponierungsrechner hilft Ihnen, eine Transponierung für jede Matrix zu finden.
Finden Sie die Hypotenuse für alle Arten von Dreiecken ganz einfach mit unserem kostenlosen Mathematikrechner heraus!
Berechnen Sie einfach trigonometrische Werte Sin, Cos, Tan, Cot, Sec und Csc mit unserem kostenlosen Online-Rechner!
Finden Sie ganz einfach die rechte Seite und den Winkel eines Dreiecks mit unserem kostenlosen Online-Rechner heraus!
Berechnen Sie Hypotenuse, Maße und Verhältnis ganz einfach mit unserem 45 45 90 Dreiecksrechner.
Berechnen Sie Matrixmultiplikationen ganz einfach mit unserem kostenlosen Online-Mathematikrechner!
Berechnen Sie einfach den Mittelwert von Zahlen mit unserem kostenlosen Online-Mathe-Rechner
Dieses Tool generiert eine echte Zufallszahl zwischen zwei beliebigen Zahlen.
Dieser Rechner berechnet die Fehlerquote für Umfragen basierend auf Stichprobengröße und -anteil. Es ermöglicht Ihnen auch, das gewünschte Vertrauensniveau einzustellen.
Dieses Online-Tool berechnet den Winkel zwischen zwei Vektoren und bietet alle möglichen Vektorkombinationen.
Dieser Rechner hilft Ihnen, das LCM oder LCD für einen bestimmten Satz von Zahlen zu finden.
Dieser Online-Rechner berechnet die in Fuß gemessene Fläche einer Form. Funktioniert mit allen Formen und Maßeinheiten!
Dies ist ein Online-Rechner, der Exponenten berechnen kann.
Dieses Online-Tool berechnet den Rest einer Division.
Berechnen Sie ganz einfach den direkten Anteil von Zahlen mit unserem kostenlosen Dreisatz-Rechner.
Quadratische Gleichungen sind alle Polynomalgebra zweiten Grades mit der folgenden Form in der Algebra.
Mit diesem Summennotationsrechner können Sie schnell die Summe einer Mengenzahl berechnen, die auch als Sigma bekannt ist. Daher wird es oft als Sigma-Rechner bezeichnet. Es gibt Ihnen auch eine Probe aus der Reihe, um eine Summe zu sein. Es kann im einfachen Modus verwendet werden, um eine einfache Summe mit einem gegebenen Satz von Zahlen zu berechnen.
Dies ist ein kostenloses Online-Tool, das den Umfang verschiedener Formen berechnet.
Dies ist ein Rechner, der den Z-Score eines Datensatzes berechnet.
Mit diesem Fibonacci-Rechner können die Terme der Fibonacci-Folge beliebig berechnet werden.
Es ist ein kostenloser Rechner, der Ihnen helfen kann, das Volumen jeder Kapsel zu ermitteln.
Es ist ein kostenloser Rechner, der Ihnen helfen kann, das Volumen verschiedener Formen zu ermitteln.
Es ist ein kostenloser Rechner, mit dem Sie das Volumen eines beliebigen dreieckigen Prismas ermitteln können.
Es ist ein kostenloser Rechner, der Ihnen helfen kann, das Volumen einer Kiste zu ermitteln.
Dieser Rechner berechnet das Kegelvolumen und kann zur Lösung von Schulproblemen verwendet werden.
Dies ist ein Online-Tool, das das Volumen eines beliebigen Würfels berechnet.
Dies ist ein Online-Tool, das das Volumen eines Zylinders berechnet.
Dies ist ein Online-Rechner, mit dem Sie die Skalierungsfaktor-Dilatation eines Objekts berechnen können.
Der Shannon-Biodiversitätsindex-Rechner kann verwendet werden, um die Artenvielfalt in einer Gemeinschaft zu berechnen. Ökologen können den Shannon-Diversitätsindex verwenden, um nützliche Informationen über den Lebensraum zu erhalten.
Verwenden Sie diesen Bayes-Theorem-Rechner online, um die Wahrscheinlichkeit eines Ereignisses zu bestimmen, das von einem anderen abhängig ist. Diese Berechnung berücksichtigt die vorherige Wahrscheinlichkeit von A, die Wahrscheinlichkeiten B bedingt und A bedingt und A bedingt.
Mit dem Antilog-Rechner können Sie die umgekehrte Logarithmusfunktion berechnen. Berechnen Sie den Antilogarithmus für jede Zahl mit jeder Basis, egal ob es 10, natürlicher Antilog oder eine andere Zahl ist.
Mit diesem erstaunlichen Tool können Sie e mit einer beliebigen Zahl Ihrer Wahl berechnen.
Dieser Rechner zeigt Ihnen, ob eine Zahl eine Primzahl hat oder ob es sich um eine zusammengesetzte Zahl handelt.
Der exponentielle Wachstumsrechner berechnet den Endpreis einer Menge basierend auf ihren Anfangswerten, der Wachstumsrate und der Zeit.
Berechnen Sie die Stichprobengröße basierend auf der Populationsgröße, dem Konfidenzniveau und der Fehlerspanne.
Dieser Online-Rechner zeigt das inverse Logarithmus der eingegebenen Zahl und Basis an.
Mit dem Poisson-Verteilungsrechner können Sie die Wahrscheinlichkeit bestimmen, dass ein Ereignis während eines bestimmten Zeitraums mehrmals auftritt.
Dieser Rechner hilft Ihnen, die multiplikative Inverse einer ganzen Zahl, einer Dezimalzahl, eines Bruchs oder einer gemischten Zahl zu finden.
Dieser Rechner rechnet Testnoten in Prozent um. Es kann verwendet werden, um schnell den Prozentsatz einer oder mehrerer Testnoten (Noten) und die maximale Anzahl von Noten zu berechnen.
Dieser Rechner kann verwendet werden, um die Abmessungen von Bildern zu bestimmen, wenn Sie deren Größe ändern.
Der empirische Regelrechner, auch bekannt als "68 95 99 Regelberechnung", ist ein Tool, mit dem Sie die Bereiche bestimmen können, die entweder 1 oder 2 Standardabweichungen oder 3 Standardabweichungen sind. Dieser Rechner zeigt Ihnen die Bereiche, in denen 68, 95 bzw. 99,7 % der normalverteilten Daten liegen.
Mit diesem unglaublichen Tool können Sie den p-Wert ermitteln. Sie können Teststatistiken verwenden, um zu bestimmen, welcher p-Wert einseitig und welcher zweiseitig ist.
Es ist ein kostenloser Rechner, der Ihnen helfen kann, das Volumen einer Kugel zu ermitteln.
Mit diesem Online-Rechner können Sie den NPV (Nettogegenwartswert) einer Investition berechnen. Die Berechnung basiert auf der Anfangsinvestition und dem Abzinsungssatz. Sie können auch interne Renditen (IRR), Bruttorenditen und Netto-Cashflows berechnen.
Verwenden Sie diesen Rechner, um herauszufinden, wie eine prozentuale Verringerung um einen beliebigen Betrag das Ergebnis verändert. Geben Sie einfach den ursprünglichen Wert, die prozentuale Abnahme und den neuen Wert ein, um die Änderung zu berechnen.
Unser intuitives Tool lässt Sie aus verschiedenen Formen wählen und berechnet deren Fläche im Handumdrehen.
Mit dem Wahrscheinlichkeitsrechner können Sie die Wahrscheinlichkeitsbeziehungen zwischen zwei separaten Ereignissen untersuchen. Auf diese Weise können Sie besser verstehen, wie Ereignisse zusammenhängen, und dadurch Vorhersagen genauer machen.
Verwenden Sie unseren Bruch-zu-Dezimal-Rechner, um Brüche einfach in Dezimalzahlen umzuwandeln und wieder zurück!
Ermitteln Sie die Faktoren einer beliebigen Zahl mit unserem Faktorrechner
Wandeln Sie mit unserem einfachen Tool einen Bruch in einen Rechner mit gemischten Zahlen um