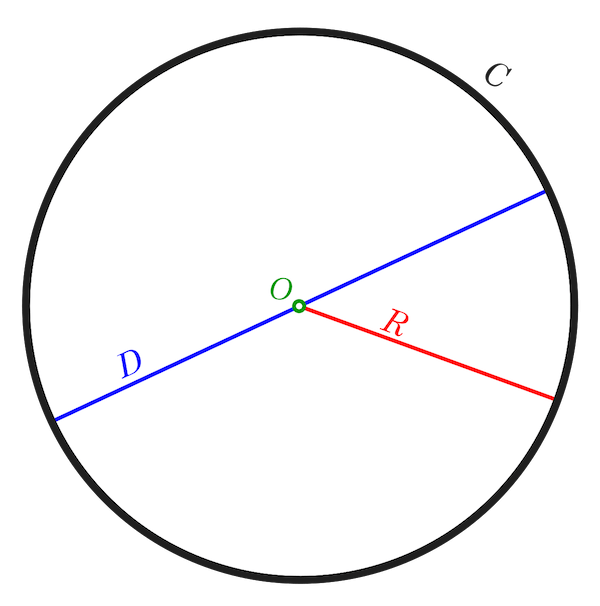
Ympyrän Ympärysmitan Laskin
Tämän ilmaisen ympyrän ympärysmittalaskurin avulla voit laskea ympyrän säteen, ympyrän halkaisijan, ympyrän kehän ja ympyrän alueen.
Sisällysluettelo
| ◦Kuinka käyttää ympyrän ympärysmittalaskuria? |
| ◦Mikä on ympärysmitta? |
| ◦Mikä on ympyrä? |
| ◦Asiaankuuluvat ympyräkaavat |
| ◦Ympärysmittakaava |
| ◦Piireihin liittyvät termit |
| ◦Ympyrän historia |
Kuinka käyttää ympyrän ympärysmittalaskuria?
Mikä on ympärysmitta?
Mikä on ympyrä?
Asiaankuuluvat ympyräkaavat
Ympärysmittakaava
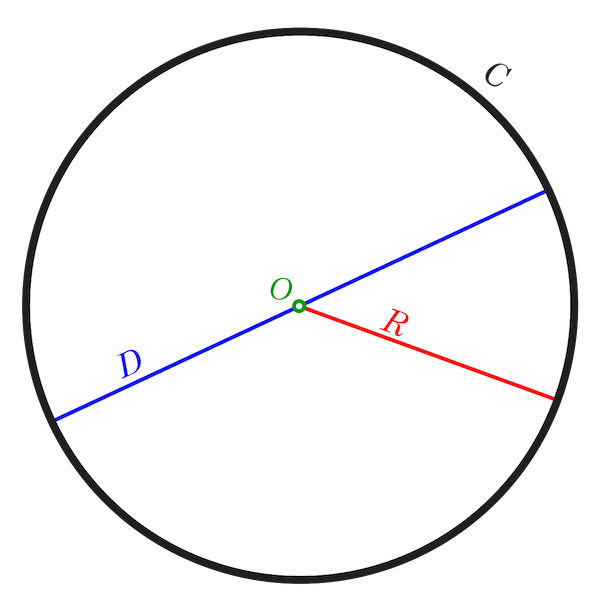
Piireihin liittyvät termit
Ympyrän historia

Ympyrän Ympärysmitan Laskin Suomi
Muut matemaattiset laskimet
Vektorin ristitulon laskin laskee sinulle kahden vektorin ristitulon kolmiulotteisessa avaruudessa.
30 60 90 kolmiolaskimen avulla voit ratkaista erityisen suorakulmion.
Tämän odotusarvon laskimen avulla voit laskea muuttujasarjan odotusarvon sekä muuttujien todennäköisyydet.
Tämä tieteellinen laskin tarjoaa yksinkertaisia ja edistyneitä matemaattisia toimintoja helppokäyttöisessä sovelluksessa.
Tämä ilmainen laskin antaa sinulle tietyn tietojoukon keskihajonnan, varianssin, keskiarvon ja summan.
Tämä prosenttilaskin on ilmainen online-laskin prosenttiosuuksien laskemiseksi. Selvitä, mikä on X% Y: stä?
Tätä ilmaista murtolaskuria voidaan käyttää tuloksen löytämiseen kahden yleisen jakeen yhteenlaskemiseen, vähentämiseen, kertomiseen ja jakamiseen.
Selvitä lempireseptisi oikeat mitat tällä ilmaisella laskimella, joka muuntaa kilot kuppeiksi helposti! Toimii US Cupin ja UK cupin kanssa!
Määritä tietyn kulman kaksoiskulmavaste tämän ilmaisen laskimen avulla! Lisätietoja kaksoiskulmakaavasta.
Tämä ilmainen laskin laskee toisen, kolmannen ja korkeamman eksponentin ja juuret. Kaava on myös saatavilla.
Selvitä kolmion pinta -ala helposti ilmaisella kolmioaluelaskurillamme! Voit laskea pohjan ja korkeuden, kolmen eri sivun ja paljon muuta. Toimii kulmien ja radiaanien kanssa!
Selvitä pääkulmat kotipisteiden kulmalaskurimme avulla! Työskentelee asteiden ja radiaanien kanssa selvittääksesi positiiviset ja negatiiviset välit!
Laske matemaattiset pistetuotteet, skalaarituotteet ja pisteiden tuotekulmat helposti vektoreillesi.
Selvitä suoran tai kolmion keskipisteet helposti keskipistelaskurillamme! Tämä sivu opettaa sinulle myös arvokkaan keskipisteen kaavan!
Selvitä oikea määrä merkittäviä numeroita helposti numerotyökalumme avulla!
Selvitä ympyrän kaaren pituus helposti tämän online -matematiikkalaskurin avulla!
Laske pistearvio helposti ilmaisen online -työkalumme avulla!
Laske prosentuaalinen lisäys helposti ilmaisella online -laskimellamme!
Laske prosentuaalinen ero heti matemaattisen prosenttierolaskurimme avulla!
Tämä ilmainen online -laskin laskee lineaarisen interpoloinnin ja lineaarisen ekstrapoloinnin. Se tarjoaa myös lineaarisen yhtälön kaltevuuden.
Selvitä ortonormaalimatriisi ja ylempi kolmionmuotoinen matriisi helposti ilmaisella online -QR -hajoamislaskurillamme!
Tämä matriisin transponointilaskin auttaa sinua löytämään transponoinnin mille tahansa matriisille.
Selvitä hypotenuusa kaikenlaisille kolmioille helposti ilmaisella matemaattisella laskimellamme!
Laske helposti trigonometriset arvot Sin, Cos, Tan, Cot, Sec ja Csc ilmaisella online-laskimellamme!
Selvitä helposti kolmion oikea puoli ja kulma ilmaisella verkkolaskimellamme!
Laske hypotenuusa, mitat ja suhde helposti 45 45 90 kolmiolaskimellamme.
Laske matriisikertoimet helposti ilmaisella online-matematiikan laskimellamme!
Laske lukujen keskiarvo helposti ilmaisella online-matematiikan laskimellamme
Tämä työkalu luo todella satunnaisen luvun minkä tahansa kahden luvun väliin.
Tämä laskin laskee kyselyiden virhemarginaalin otoskoon ja osuuden perusteella. Sen avulla voit myös asettaa halutun luottamustason.
Tämä online-työkalu laskee kahden vektorin välisen kulman ja sisältää kaikki mahdolliset vektoriyhdistelmät.
Tämä laskin auttaa sinua löytämään LCM- tai LCD-näytön tietylle numerojoukolle.
Tämä online-laskin laskee muodon alueen jalkoina mitattuna. Toimii kaikkien muotojen ja mittayksiköiden kanssa!
Tämä on online-laskin, joka voi laskea eksponentit.
Tämä online-työkalu laskee jaon loppuosan.
Laske helposti suorat osuudet numeroista ilmaisella kolmen säännön laskimellamme.
Neliöyhtälöt ovat mitä tahansa toisen asteen polynomialgebraa, jolla on seuraava muoto algebrassa.
Tämän summauslaskimen avulla voit nopeasti laskea joukon luvun summan, joka tunnetaan myös nimellä Sigma. Siksi sitä kutsutaan usein sigma-laskimeksi. Se antaa sinulle myös näytteen sarjasta summaksi. Sitä voidaan käyttää yksinkertaisessa tilassa yksinkertaisen summan laskemiseen käyttämällä annettua numerosarjaa.
Tämä on ilmainen online-työkalu, joka laskee eri muotojen kehän.
Tämä on laskin, joka laskee tietojoukon z-pisteen.
Tätä Fibonacci-laskinta voidaan käyttää Fibonacci-sekvenssin termien mielivaltaiseen laskemiseen.
Se on ilmainen laskin, jonka avulla voit selvittää minkä tahansa kapselin tilavuuden.
Se on ilmainen laskin, jonka avulla voit löytää eri muotojen tilavuuden.
Se on ilmainen laskin, joka voi auttaa sinua löytämään minkä tahansa kolmion muotoisen prisman tilavuuden.
Se on ilmainen laskin, jonka avulla voit laskea laatikon tilavuuden.
Tämä laskin laskee kartion tilavuuden ja sitä voidaan käyttää koulutehtävien ratkaisemiseen.
Tämä on online-työkalu, joka laskee minkä tahansa kuution tilavuuden.
Tämä on online-työkalu, joka laskee sylinterin tilavuuden.
Tämä on online-laskin, jonka avulla voit laskea kohteen mittakertoimen laajenemisen.
Shannonin biodiversiteettiindeksilaskuria voidaan käyttää yhteisön lajien monimuotoisuuden laskemiseen. Ekologit voivat käyttää Shannonin monimuotoisuusindeksiä saadakseen hyödyllistä tietoa elinympäristöstä.
Käytä tätä Bayesin lauselaskuria verkossa määrittääksesi todennäköisyyden sellaiselle tapahtumalle, joka on riippuvainen toisesta. Tämä laskelma ottaa huomioon A:n ennakkotodennäköisyyden, todennäköisyydet B ehdollisen ja A:n ehdollisen todennäköisyyden sekä A ehdollisen todennäköisyyden.
Antilog-laskimella voit laskea käänteisen logaritmifunktion. Laske antilogaritmi mille tahansa luvulle, jolla on mikä tahansa kanta, olipa se sitten 10, luonnollinen antilog tai jokin muu luku.
Tämän hämmästyttävän työkalun avulla voit laskea e:n minkä tahansa valitsemasi luvun potenssiin.
Tämä laskin näyttää, onko luvulla alkuluku vai onko se yhdistelmä.
Eksponentiaalinen kasvulaskin laskee määrän lopullisen hinnan sen alkuarvojen, kasvunopeuden ja ajan perusteella.
Laske otoskoko populaation koon, luottamustason ja virhemarginaalin perusteella.
Tämä online-laskin näyttää syötetyn numeron ja kantaluvun käänteisen lokin.
Poisson-jakauman laskimen avulla voit määrittää tapahtuman todennäköisyyden useita kertoja tietyn ajanjakson aikana.
Tämä laskin auttaa sinua löytämään kokonaisluvun, desimaaliluvun, murtoluvun tai sekaluvun kertolaskujen käänteisluvun.
Tämä laskin muuntaa testipisteet prosentteiksi. Sen avulla voidaan nopeasti laskea yhden tai useamman koearvosanan (arvosanan) prosenttiosuus ja pisteiden enimmäismäärä.
Tämän laskimen avulla voit määrittää kuvien mitat, kun muutat niiden kokoa.
Empiirinen sääntölaskin, joka tunnetaan myös nimellä "68 95 99 sääntölaskenta", on työkalu, jonka avulla voit määrittää alueet, jotka ovat joko 1 tai 2 keskihajontaa tai 3 standardipoikkeamaa. Tämä laskin näyttää alueet, joilla normaalisti jakautuneista tiedoista on 68, 95 tai 99,7 %.
Tämän uskomattoman työkalun avulla voit löytää p-arvon. Voit käyttää testitilastoja määrittääksesi, mikä p-arvo on yksipuolinen ja mikä kaksipuolinen.
Se on ilmainen laskin, jonka avulla voit laskea pallon tilavuuden.
Tämän online-laskimen avulla voit laskea sijoituksen NPV (Net Present Value). Laskelma perustuu alkuinvestointiin ja diskonttokorkoon. Voit myös laskea sisäiset tuottoprosentit (IRR), bruttotuotot ja nettokassavirrat.
Käytä tätä laskinta selvittääksesi, kuinka prosentuaalinen vähennys millä tahansa määrällä muuttaa tulosta. Syötä vain alkuperäinen arvo, prosentuaalinen vähennys ja uusi arvo laskeaksesi muutoksen.
Intuitiivisen työkalumme avulla voit valita eri muodoista ja laskea niiden alueen silmänräpäyksessä.
Todennäköisyyslaskurin avulla voit tutkia kahden erillisen tapahtuman välisiä todennäköisyyssuhteita. Näin saat paremman käsityksen siitä, miten tapahtumat liittyvät toisiinsa, ja tekee siten ennusteista tarkempia.
Käytä murto-desimaalilaskuriamme, jonka avulla voit helposti muuntaa murtoluvut desimaaleiksi ja takaisin!
Selvitä minkä tahansa luvun tekijät kertoimellamme
Muunna murto sekalukulaskimeksi yksinkertaisella työkalullamme