30 60 90 Triangelkalkylator
Med vår 30 60 90 triangelkalkylator kan du lösa den speciella högra triangeln.
Innehållsförteckning
Vad är en 30 60 90 triangel?
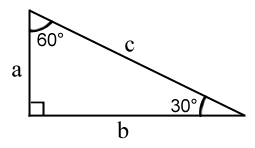
30-60-90 är en speciell typ av triangel
Vilken sida av 30 60 90 triangeln är vilken?
Triangel beräkna, hitta a, hitta b
Hur löser man den speciella högra triangeln?
Speciellt höger triangelförhållande

30 60 90 Triangelkalkylator Svenska
Andra matematiska räknare
Vector cross product calculator hittar korsprodukten av två vektorer i ett tredimensionellt utrymme.
Denna förväntade värdekalkylator hjälper dig att beräkna ett förväntat värde (även kallat medelvärde) för den angivna variabeluppsättningen med deras sannolikheter.
Denna vetenskapliga kalkylator ger enkla och avancerade matematiska funktioner i en lättanvänd app.
Denna kostnadsfria kalkylator ger dig standardavvikelsen, variansen, medelvärdet och summan av en given datamängd.
Denna procentuella kalkylator är en gratis online-kalkylator för att beräkna procentsatser. Ta reda på vad som är X% av Y?
Den här fria fraktionsräknaren kan användas för att hitta resultatet för att addera, subtrahera, multiplicera och dela två vanliga fraktioner.
Ta reda på korrekta mått för ditt favoritrecept med denna gratis kalkylator förvandlar enkelt pund till koppar! Fungerar med amerikanska koppar och brittiska koppar!
Använd den här kostnadsfria cirkelomkretsen för att beräkna cirkelradie, cirkeldiameter, cirkelomkrets och cirkelarea.
Bestäm dubbelvinkelekvivalenten för en given vinkel med denna gratis räknare! Hitta mer information om dubbelvinkelformeln.
Denna gratis räknare beräknar den andra, tredje och högre exponenten och rötterna. Formel finns också.
Ta reda på området för triangeln enkelt med vår gratis triangelområdesräknare! Du kan beräkna med bas och höjd, tre olika sidor och många fler. Fungerar med vinklar och radianer!
Ta reda på koterminalvinklar med vår coterminalvinkelräknare! Arbetar med grader och radianer för att ta reda på positiva och negativa koterminalvinklar!
Beräkna matematiska prickprodukter, skalärprodukter och punktproduktvinklar enkelt för dina vektorer.
Ta reda på mittpunkter för en linje eller en triangel enkelt med vår mittpunktsräknare! Denna sida kommer också att lära dig värdefull mittpunktsformel!
Ta reda på rätt mängd signifikanta siffror i ditt nummer enkelt med vårt signifikanta figurverktyg!
Ta reda på längden på en cirkelbåge med den här matematiska kalkylatorn online!
Beräkna poänguppskattning enkelt med vårt gratis onlineverktyg!
Beräkna en procentuell ökning enkelt med vår gratis onlinekalkylator!
Beräkna procentuell skillnad direkt med vår matematiska procentuella skillnadskalkylator!
Denna gratis onlinekalkylator beräknar den linjära interpoleringen och den linjära extrapolationen. Det ger också lutningen för den linjära ekvationen.
Ta reda på ortonormal matris och övre triangulär matris enkelt med vår gratis online QR -sönderdelningsräknare!
Denna matris transponeringskalkylator hjälper dig att hitta en transponering för vilken matris som helst.
Ta reda på hypotenusa för alla typer av trianglar enkelt med vår gratis matematikkalkylator!
Beräkna enkelt trigonometriska värden Sin, Cos, Tan, Cot, Sec och Csc med vår gratis onlineräknare!
Ta reda på enkelt höger sida och vinkel på en triangel med vår gratis onlineräknare!
Beräkna hypotenusa, mått och förhållande enkelt med vår 45 45 90 triangelräknare.
Beräkna matrismultiplikationer enkelt med vår gratis matematikkalkylator online!
Beräkna enkelt medelvärde av siffror med vår kostnadsfria matematikkalkylator online
Detta verktyg genererar ett verkligt slumpmässigt tal mellan två valfria tal.
Denna kalkylator beräknar felmarginalen för undersökningar baserat på urvalsstorlek och andel. Det låter dig också ställa in önskad nivå av självförtroende.
Detta onlineverktyg beräknar vinkeln mellan två vektorer och har alla möjliga vektorkombinationer.
Denna kalkylator hjälper dig att hitta LCM eller LCD för en viss uppsättning siffror.
Denna online-kalkylator beräknar arean av en form mätt i fot. Fungerar med alla former och måttenheter!
Detta är en onlineräknare som kan beräkna exponenter.
Detta onlineverktyg beräknar resten av en division.
Beräkna enkelt direkt andel av siffror med vår kostnadsfria Rule of Three-kalkylator.
Andragradsekvationer är vilken polynomalgebra som helst av andra graden som har följande form i algebra.
Denna summeringsnotationsräknare låter dig snabbt beräkna summeringen av ett uppsättningsnummer, även känt som Sigma. Därför kallas det ofta en sigma-räknare. Det ger dig också ett prov från serien för att vara en summa. Den kan användas i enkelt läge för att beräkna en enkel summa med en given uppsättning siffror.
Detta är ett gratis onlineverktyg som kommer att räkna ut omkretsen av olika former.
Detta är en kalkylator som beräknar z-poängen för en datamängd.
Denna Fibonacci-räknare kan användas för att beräkna termerna godtyckligt för Fibonacci-sekvensen.
Det är en gratis kalkylator som kan hjälpa dig att hitta volymen på vilken kapsel som helst.
Det är en gratis kalkylator som kan hjälpa dig att hitta volymen av olika former.
Det är en gratis kalkylator som kan hjälpa dig att hitta volymen på ett triangulärt prisma.
Det är en gratis kalkylator som kan hjälpa dig att hitta volymen på en låda.
Denna kalkylator beräknar konvolymen och kan användas för att lösa skolproblem.
Detta är ett onlineverktyg som beräknar volymen av en kub.
Detta är ett onlineverktyg som beräknar volymen på en cylinder.
Detta är en onlineräknare som hjälper dig att beräkna skalfaktorns utvidgning av ett föremål.
Shannon biodiversitetsindexberäknare kan användas för att beräkna mångfalden av arter i ett samhälle. Ekologer kan använda Shannon diversity index för att få användbar information om livsmiljöer.
Använd denna Bayes-satskalkylator online för att bestämma sannolikheten för en händelse som är villkorad av en annan. Denna beräkning tar hänsyn till den tidigare sannolikheten för A, sannolikheterna B villkorad och A villkorad, och A villkorad.
Antilog-kalkylatorn låter dig beräkna den inversa logaritmfunktionen. Beräkna antilogaritmen för valfritt tal med valfri bas, oavsett om det är 10, naturlig antilog eller ett annat tal.
Detta fantastiska verktyg låter dig beräkna e till styrkan av vilket tal du väljer.
Denna kalkylator visar dig om ett tal har ett primtal eller om det är ett sammansatt tal.
Den exponentiella tillväxtkalkylatorn beräknar slutpriset för en kvantitet baserat på dess initiala värden, tillväxttakt och tid.
Beräkna urvalsstorleken baserat på populationens storlek, konfidensnivå och felmarginal.
Den här online-kalkylatorn visar den omvända loggen för antalet och den angivna basen.
Poisson-fördelningskalkylatorn låter dig bestämma sannolikheten för att en händelse inträffar ett antal gånger under en viss tidsram.
Den här kalkylatorn hjälper dig att hitta den multiplikativa inversen av ett heltal, en decimal, en bråkdel eller ett blandat tal.
Denna kalkylator konverterar testbetyg till procent. Den kan användas för att snabbt beräkna procentandelen av ett eller flera provbetyg (betyg) och det maximala antalet betyg.
Denna kalkylator kan användas för att bestämma dimensionerna på bilder när du ändrar storlek på dem.
Den empiriska regelkalkylatorn, även känd som en "68 95 99 regelberäkning", är ett verktyg som låter dig bestämma intervallen som är antingen 1 eller 2 standardavvikelser eller 3 standardavvikelser. Den här kalkylatorn visar intervallen inom vilka 68, 95 eller 99,7 % av normalfördelade data.
Detta otroliga verktyg låter dig hitta p-värdet. Du kan använda teststatistik för att avgöra vilket p-värde som är ensidigt och vilket som är dubbelsidigt.
Det är en gratis kalkylator som kan hjälpa dig att hitta volymen på en sfär.
Denna online-kalkylator låter dig beräkna NPV (netto nuvärde) för en investering. Beräkningen baseras på den initiala investeringen och diskonteringsräntan. Du kan också beräkna Internal Rates of Return (IRR), bruttoavkastning och nettokassaflöden.
Använd den här kalkylatorn för att ta reda på hur en procentuell minskning med valfritt belopp kommer att förändra resultatet. Ange bara det ursprungliga värdet, den procentuella minskningen och det nya värdet för att beräkna ändringen.
Vårt intuitiva verktyg låter dig välja mellan olika former och beräknar deras yta på ett ögonblick.
Sannolikhetsberäknaren låter dig utforska sannolikhetsförhållandena mellan två separata händelser. Detta gör att du kan få en bättre förståelse för hur händelser hänger ihop och gör förutsägelser mer exakta.
Använd vår kalkylator för bråk till decimal för att enkelt konvertera bråk till decimaler och tillbaka igen!
Ta reda på faktorerna för alla tal med vår faktorräknare
Konvertera en bråkdel till en räknare med blandade tal med vårt enkla verktyg