Matrični Kalkulator Za Prenos
Ta matrični kalkulator transponiranja vam pomaga najti prenos za katero koli matriko.
Kazalo
Kako uporabljati matrični kalkulator transponiranja?
Kaj je transponiranje matrike?

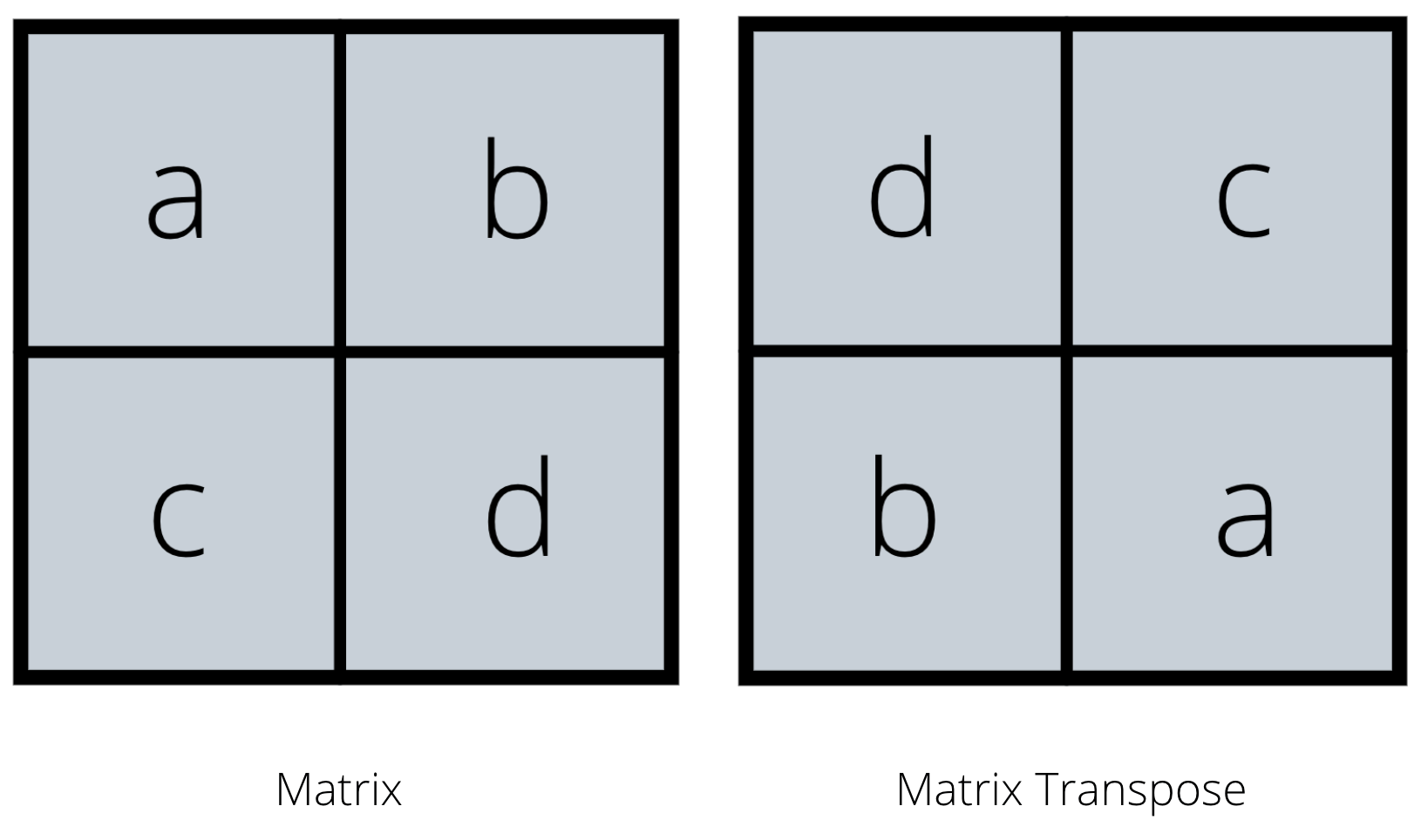
Kako ročno izračunati prenos matrike?
Za kaj se uporablja prenos matrike?
Lastnosti prenosov
1) Prenos skalarnega večkratnika
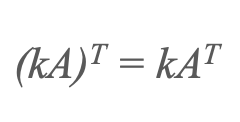
2) Prenos vsote
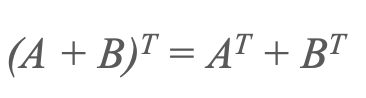
3) Prenos izdelka
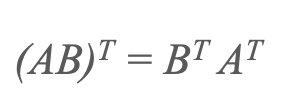

4) Prenos prenosa
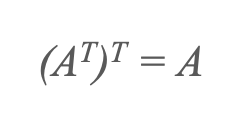
Različne vrste matric
1) Matrika vrstice in stolpca

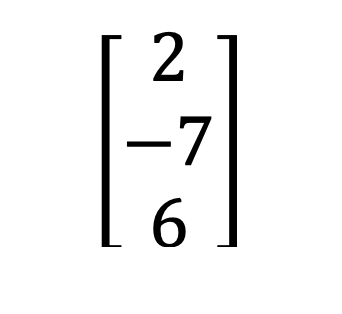
2) Pravokotna in kvadratna matrika
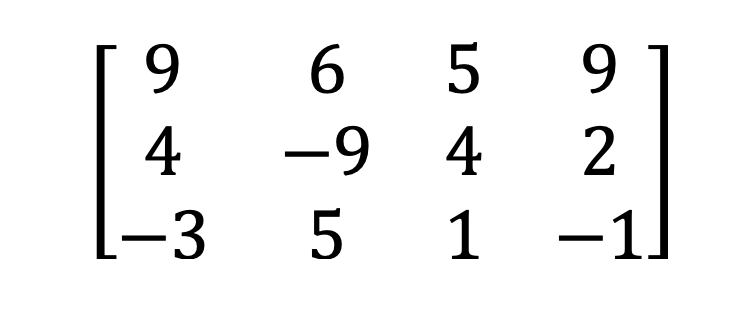
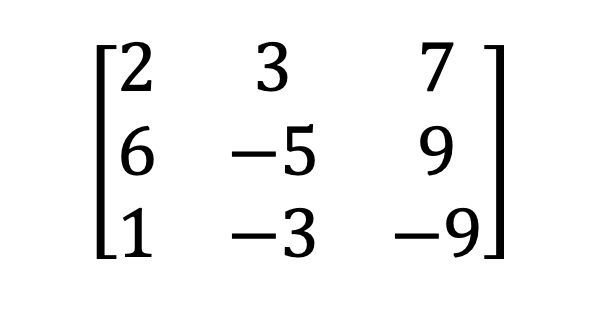
3) Singularna in ne-singularna matrika
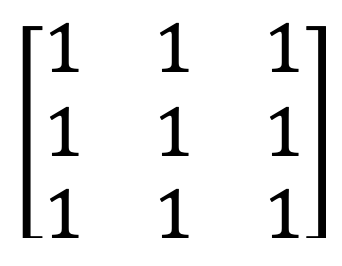
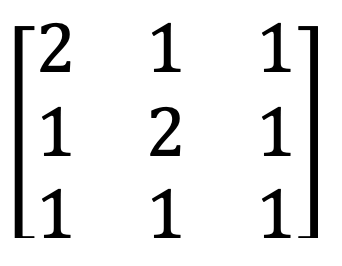
4) Identitetna matrika
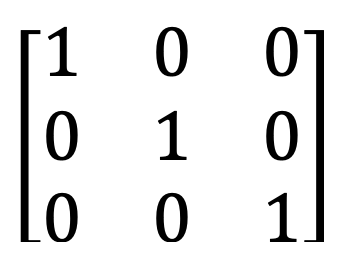
5) Matrika enot
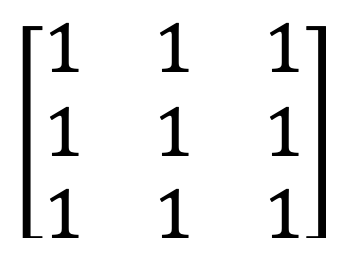
6) Ničelna matrika
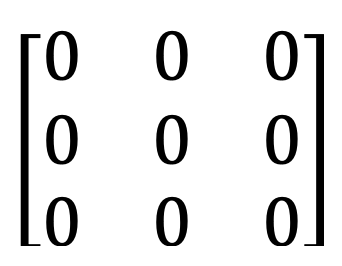
7) Diagonalna matrika in skalarna matrika
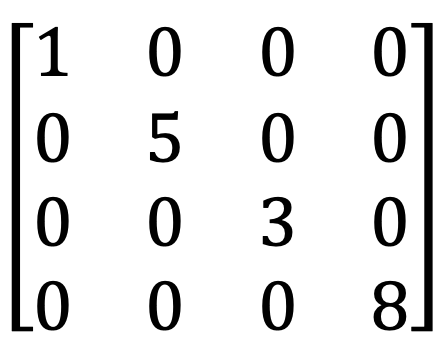

8) Zgornja in spodnja trikotna matrika

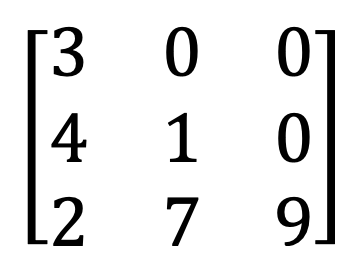
9) Simetrična in poševno-simetrična matrika
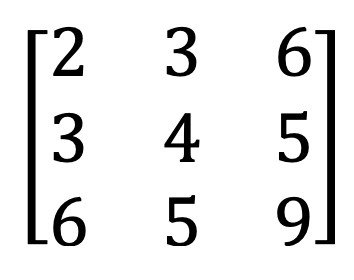
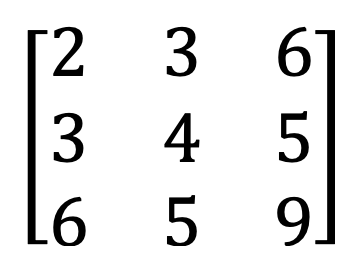
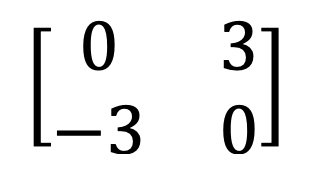
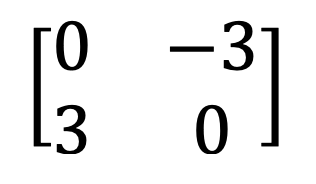
10) Logična matrika
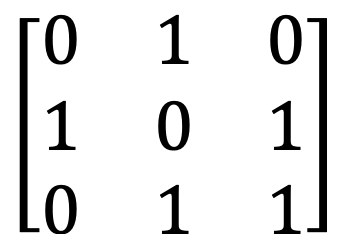
11) Stohastične matrice

12) Ortogonalna matrika
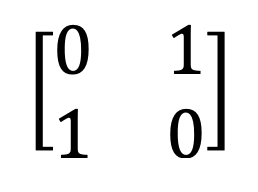
Zgodovina prenosa

Matrični Kalkulator Za Prenos Slovenski
Drugi matematični kalkulatorji
Vektorski kalkulator za navzkrižne izdelke najde trosmer dva vektorja v tridimenzionalnem prostoru.
Z našim trikotnim kalkulatorjem 30 60 90 lahko rešite poseben pravokotni trikotnik.
Ta kalkulator pričakovanih vrednosti vam pomaga izračunati pričakovano vrednost (imenovano tudi srednja vrednost) danega nabora spremenljivk z njihovimi verjetnostmi.
Ta znanstveni kalkulator ponuja preproste in napredne matematične funkcije v enostavni aplikaciji.
Ta brezplačni kalkulator vam poda standardni odklon, varianco, povprečje in vsoto danega niza podatkov.
Ta kalkulator odstotkov je brezplačen spletni kalkulator za izračun odstotkov. Ugotovite, koliko je X% Y?
S tem kalkulatorjem prostih ulomkov lahko poiščemo rezultat za seštevanje, odštevanje, množenje in deljenje dveh pogostih ulomkov.
S tem brezplačnim kalkulatorjem poiščite pravilne mere za vaš najljubši recept, ki zlahka pretvori funte v skodelice! Deluje z ameriškimi in britanskimi skodelicami!
S tem brezplačnim kalkulatorjem obsega kroga izračunajte polmer kroga, premer kroga, obseg kroga in površino kroga.
S tem brezplačnim kalkulatorjem določite dvojni kot ekvivalenta danega kota! Poiščite več informacij o formuli dvojnega kota.
Ta brezplačni kalkulator izračuna drugi, tretji in višji eksponent in korenine. Na voljo je tudi formula.
Z našim brezplačnim kalkulatorjem površine trikotnika enostavno odkrijte območje trikotnika! Izračunate lahko z osnovo in višino, tremi različnimi stranicami in še veliko več. Deluje z koti in radiani!
Odkrijte koterminalne kote z našim kalkulatorjem koterminalnega kota! Deluje s stopinjami in radiani, da ugotovi pozitivne in negativne koterminalne kote!
Za svoje vektorje enostavno izračunajte matematične pikčaste izdelke, skalarne izdelke in kote točkovnih produktov.
Z našim kalkulatorjem srednjih točk enostavno poiščite vmesne točke za črto ali trikotnik! Ta stran vas bo naučila tudi dragocene formule za srednjo točko!
Z našim orodjem za pomembne številke preprosto ugotovite pravilno količino pomembnih številk v svojem številu!
S tem spletnim matematičnim kalkulatorjem enostavno ugotovite dolžino krožnega loka!
Z našim brezplačnim spletnim orodjem enostavno izračunajte oceno točke!
Z našim brezplačnim spletnim kalkulatorjem enostavno izračunajte odstotek povečanja!
Izračunajte odstotno razliko takoj z našim matematičnim kalkulatorjem odstotne razlike!
Ta brezplačni spletni kalkulator izračuna linearno interpolacijo in linearno ekstrapolacijo. Zagotavlja tudi naklon linearne enačbe.
Z našim brezplačnim spletnim kalkulatorjem razgradnje QR enostavno odkrijte ortonormalno matriko in zgornjo trikotno matriko!
Z našim brezplačnim matematičnim kalkulatorjem enostavno ugotovite hipotenuzo za vse vrste trikotnikov!
Z našim brezplačnim spletnim kalkulatorjem enostavno izračunajte trigonometrične vrednosti Sin, Cos, Tan, Cot, Sec in Csc!
Z našim brezplačnim spletnim kalkulatorjem enostavno ugotovite desno stran in kot trikotnika!
Hipotenuzo, meritve in razmerje enostavno izračunajte z našim kalkulatorjem trikotnika 45 45 90.
Preprosto izračunajte množenje matrik z našim brezplačnim spletnim matematičnim kalkulatorjem!
Z našim brezplačnim spletnim matematičnim kalkulatorjem enostavno izračunajte srednje povprečje številk
To orodje ustvari resnično naključno število med poljubnima dvema številkama.
Ta kalkulator izračuna stopnjo napake za raziskave na podlagi velikosti vzorca in deleža. Prav tako vam omogoča, da nastavite želeno raven zaupanja.
To spletno orodje izračuna kot med dvema vektorjema in ima vse možne vektorske kombinacije.
Ta kalkulator vam bo pomagal najti LCM ali LCD za določen niz številk.
Ta spletni kalkulator izračuna površino oblike, merjeno v čevljih. Deluje z vsemi oblikami in merskimi enotami!
To je spletni kalkulator, ki lahko izračuna eksponente.
To spletno orodje izračuna preostanek deljenja.
Z našim brezplačnim kalkulatorjem pravila treh enostavno izračunajte neposreden delež števil.
Kvadratne enačbe so katera koli polinomska algebra druge stopnje, ki ima v algebri naslednjo obliko.
Ta kalkulator zapisov seštevanja vam omogoča hitro izračun seštevanja niza števila, znanega tudi kot Sigma. Zato se pogosto imenuje sigma kalkulator. Daje vam tudi vzorec iz serije, ki je vsota. V preprostem načinu se lahko uporablja za izračun preproste vsote z uporabo danega niza številk.
To je brezplačno spletno orodje, ki bo izračunalo obseg različnih oblik.
To je kalkulator, ki izračuna z-rezultat nabora podatkov.
Ta Fibonaccijevi kalkulator se lahko uporablja za poljubno izračun izrazov Fibonaccijevega zaporedja.
Je brezplačen kalkulator, ki vam lahko pomaga najti prostornino katere koli kapsule.
Je brezplačen kalkulator, ki vam lahko pomaga najti prostornino različnih oblik.
Je brezplačen kalkulator, ki vam lahko pomaga najti prostornino katere koli trikotne prizme.
Je brezplačen kalkulator, ki vam lahko pomaga najti prostornino škatle.
Ta kalkulator izračuna prostornino stožca in se lahko uporablja za reševanje šolskih težav.
To je spletno orodje, ki bo izračunalo prostornino katere koli kocke.
To je spletno orodje, ki bo izračunalo prostornino jeklenke.
To je spletni kalkulator, ki vam bo pomagal izračunati dilatacijo faktorja skale predmeta.
Kalkulator indeksa biotske raznovrstnosti Shannon se lahko uporablja za izračun raznolikosti vrst v skupnosti. Ekologi lahko s Shannonovim indeksom raznolikosti pridobijo koristne informacije o habitatu.
Uporabite ta kalkulator Bayesovega izreka na spletu, da določite verjetnost dogodka, ki je pogojen z drugim. Ta izračun upošteva predhodno verjetnost A, pogojne verjetnosti B in A pogojne ter A pogojne.
Antilog kalkulator vam omogoča izračun funkcije inverznega logaritma. Izračunajte antilogaritem za katero koli število s katero koli osnovo, naj bo to 10, naravni antilogaritem ali drugo število.
To neverjetno orodje vam bo omogočilo, da izračunate e na moč poljubnega števila, ki ga izberete.
Ta kalkulator vam bo pokazal, ali ima število praštevilo ali je sestavljeno.
Kalkulator eksponentne rasti izračuna končno ceno količine na podlagi njenih začetnih vrednosti, stopnje rasti in časa.
Izračunajte velikost vzorca na podlagi velikosti populacije, stopnje zaupanja in stopnje napake.
Ta spletni kalkulator bo prikazal inverzni dnevnik števila in vnesene osnove.
Kalkulator Poissonove porazdelitve vam bo omogočil določitev verjetnosti, da se dogodek zgodi večkrat v določenem časovnem okviru.
Ta kalkulator vam bo pomagal najti multiplikativno inverzno celo število, decimalko, ulomek ali mešano število.
Ta kalkulator pretvori testne ocene v odstotke. Z njim lahko hitro izračunamo odstotek ene ali več testnih ocen (ocen) in največje število ocen.
Ta kalkulator lahko uporabite za določanje dimenzij slik, ko jim spremenite velikost.
Kalkulator empiričnega pravila, znan tudi kot "izračun pravila 68 95 99", je orodje, ki vam omogoča, da določite obsege, ki so 1 ali 2 standardni odkloni ali 3 standardni odkloni. Ta kalkulator vam bo pokazal obsege, v katerih je 68, 95 ali 99,7 % normalno porazdeljenih podatkov.
To neverjetno orodje vam bo omogočilo, da najdete p-vrednost. S testno statistiko lahko ugotovite, katera p-vrednost je enostranska in katera dvostranska.
Je brezplačen kalkulator, ki vam lahko pomaga najti prostornino krogle.
Ta spletni kalkulator vam bo omogočil izračun NPV (neto sedanje vrednosti) naložbe. Izračun temelji na začetni naložbi in diskontni stopnji. Izračunate lahko tudi notranje stopnje donosa (IRR), bruto donose in neto denarne tokove.
S tem kalkulatorjem ugotovite, kako bo odstotek zmanjšanja za kateri koli znesek spremenil rezultat. Preprosto vnesite prvotno vrednost, odstotek zmanjšanja in novo vrednost za izračun spremembe.
Naše intuitivno orodje vam omogoča izbiro med različnimi oblikami in izračuna njihovo površino v hipu.
Kalkulator verjetnosti vam omogoča raziskovanje razmerij verjetnosti med dvema ločenima dogodkoma. To vam omogoča, da bolje razumete, kako so dogodki povezani, in s tem naredi napovedi natančnejše.
Uporabite naš kalkulator za ulomke v decimalke za enostavno pretvorbo ulomkov v decimalke in nazaj!
Poiščite faktorje poljubnega števila z našim faktorskim kalkulatorjem
Z našim preprostim orodjem pretvorite ulomek v kalkulator mešanih števil