Maticová Transponovaná Kalkulačka
Tato kalkulačka transpozice matice vám pomůže najít transpozici pro jakoukoli matici.
Obsah
Jak používat kalkulačku transpozice matice?
Co je transpozice matice?

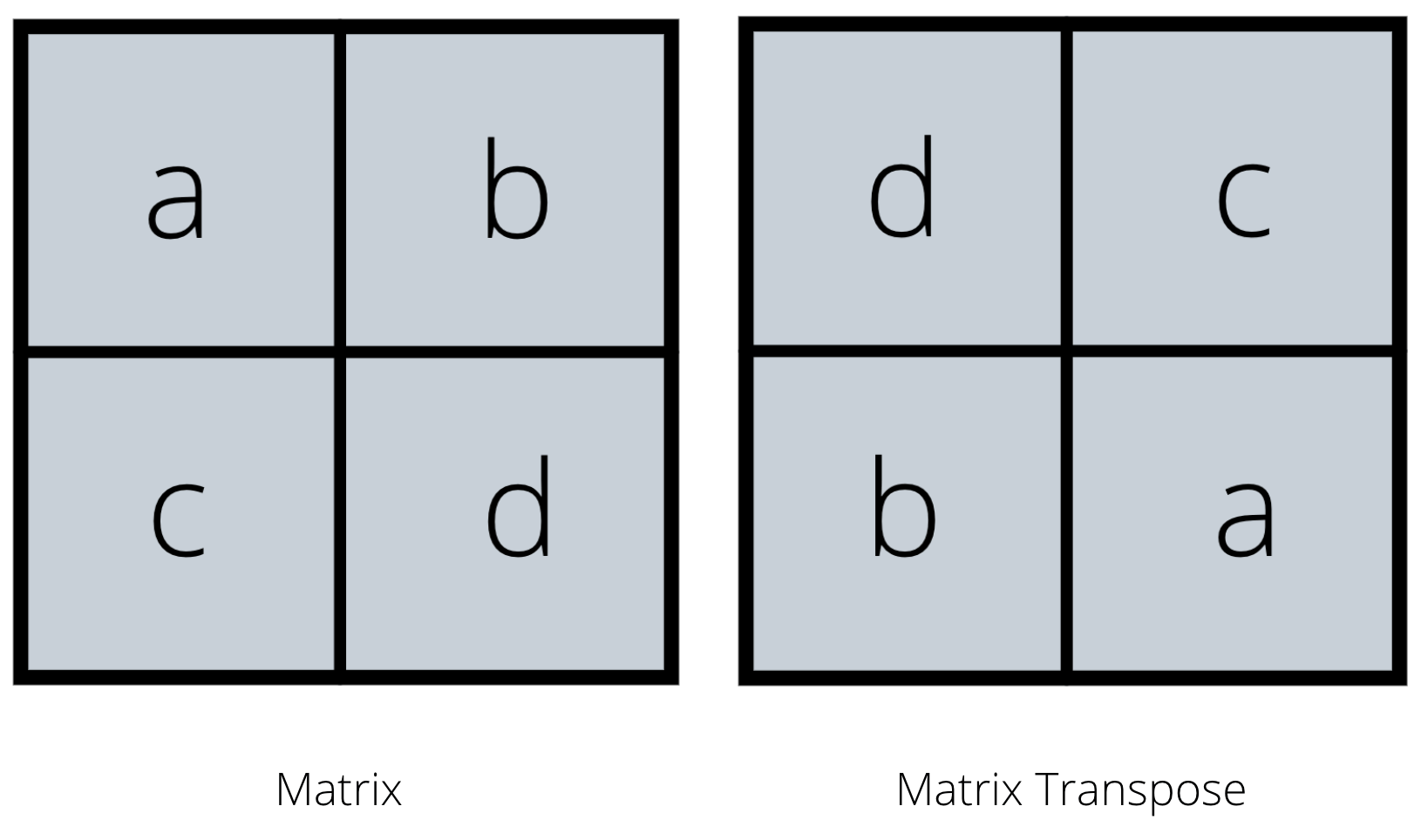
Jak ručně vypočítat transpozici matice?
K čemu slouží maticová transpozice?
Vlastnosti transpozic
1) Transponujte skalární násobek
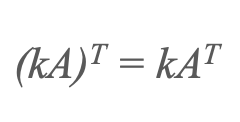
2) Transpozice částky
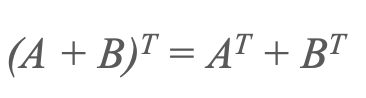
3) Transpozice produktu
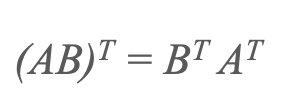

4) Transponovat transpozici
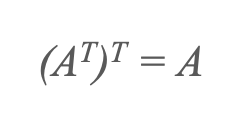
Různé typy matic
1) Matice řádků a sloupců

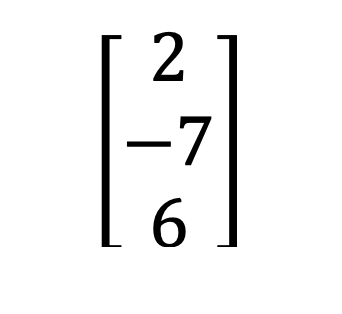
2) Obdélníková a čtvercová matice
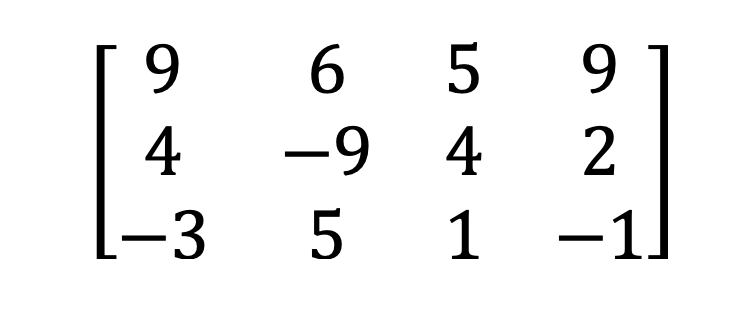
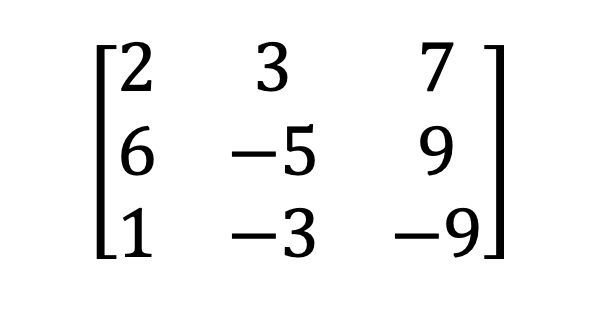
3) Singulární a nesingulární matice
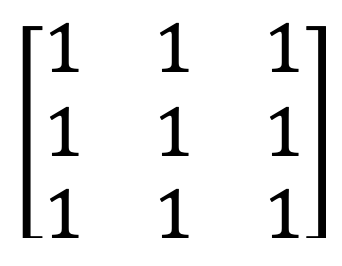
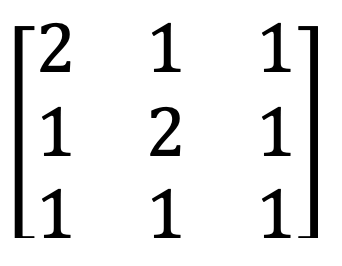
4) Matice identity
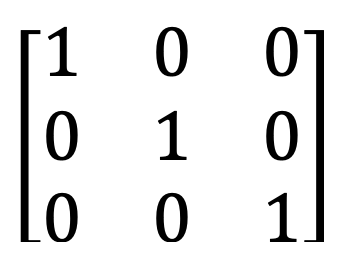
5) Matice jedniček
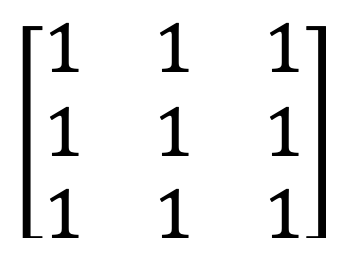
6) Nulová matice
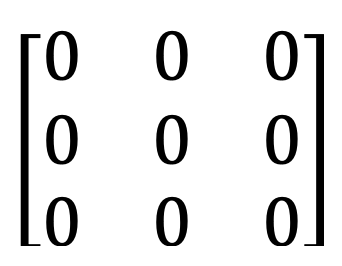
7) Diagonální matice a skalární matice
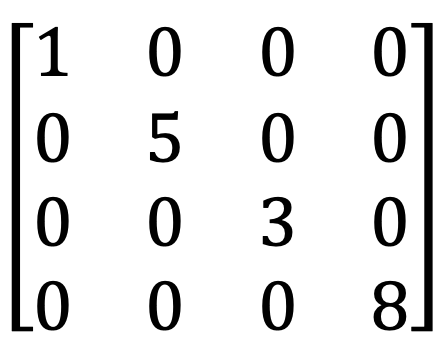

8) Horní a dolní trojúhelníková matice

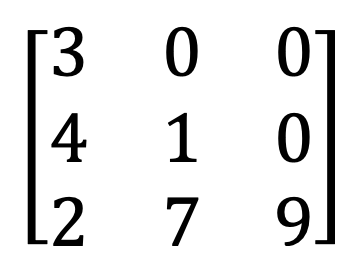
9) Symetrická a šikmá symetrická matice
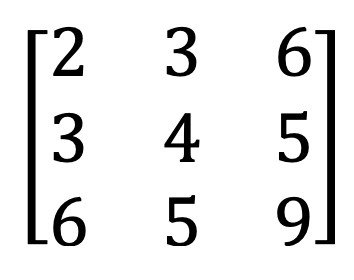
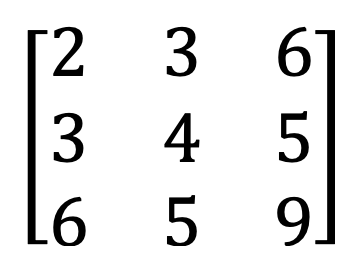
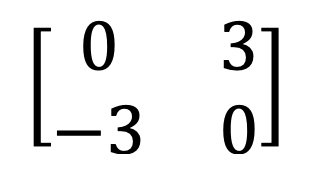
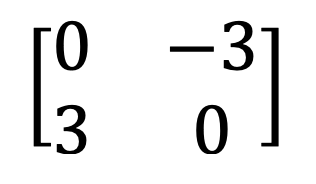
10) Booleovská matice
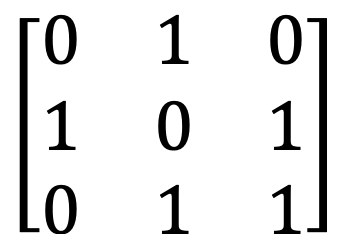
11) Stochastické matice

12) Ortogonální matice
Historie transpozice

Maticová Transponovaná Kalkulačka čeština
Jiné matematické kalkulačky
Kalkulačka vektorových křížových produktů najde křížový produkt dvou vektorů v trojrozměrném prostoru.
S naší kalkulačkou trojúhelníků 30 60 90 můžete vyřešit speciální pravý trojúhelník.
Tato kalkulačka očekávané hodnoty vám pomůže vypočítat očekávanou hodnotu (také nazývanou průměr) dané sady proměnných s jejich pravděpodobnostmi.
Tato vědecká kalkulačka poskytuje jednoduché a pokročilé matematické funkce ve snadno použitelné aplikaci.
Tato bezplatná kalkulačka vám poskytuje standardní odchylku, rozptyl, průměr a součet daného souboru dat.
Tato procentuální kalkulačka je bezplatná online kalkulačka pro výpočet procent. Zjistěte, co je X% z Y?
Tuto kalkulačku volných zlomků lze použít k vyhledání výsledku pro sčítání, odčítání, násobení a dělení dvou společných zlomků.
Zjistěte správné míry pro svůj oblíbený recept pomocí této bezplatné kalkulačky, která snadno převede libry na šálky! Funguje s poháry USA a poháry Spojeného království!
Pomocí této kalkulačky obvodu volného kruhu vypočítáte poloměr kruhu, průměr kruhu, obvod kruhu a plochu kruhu.
Pomocí této bezplatné kalkulačky určete ekvivalent dvojitého úhlu daného úhlu! Najděte více informací o vzorci dvojitého úhlu.
Tato bezplatná kalkulačka vypočítá druhé, třetí a vyšší exponenty a kořeny. K dispozici je také vzorec.
Zjistěte plochu trojúhelníku snadno pomocí naší bezplatné kalkulačky plochy trojúhelníku! Můžete počítat se základnou a výškou, třemi různými stranami a mnoha dalšími. Funguje s úhly a radiány!
Zjistěte coterminální úhly s naší kalkulačkou coterminálních úhlů! Pracuje se stupni a radiány, aby zjistil kladné a záporné koncové úhly!
Vypočítejte matematické bodové produkty, skalární součiny a úhly součinových bodů snadno pro vaše vektory.
Pomocí naší kalkulačky středových bodů snadno zjistíte středové body pro přímku nebo trojúhelník! Tato stránka vás také naučí hodnotný vzorec středního bodu!
Pomocí našeho nástroje pro významné figury snadno zjistíte správné množství významných čísel ve vašem čísle!
Zjistěte snadno délku oblouku kruhu s touto online matematickou kalkulačkou!
Vypočítejte bodový odhad snadno pomocí našeho bezplatného online nástroje!
Vypočítejte libovolné procento snadno pomocí naší bezplatné online kalkulačky!
Vypočítejte procentní rozdíl okamžitě pomocí naší matematické kalkulačky procentního rozdílu!
Tato bezplatná online kalkulačka vypočítává lineární interpolaci a lineární extrapolaci. Poskytuje také sklon lineární rovnice.
Zjistěte snadno ortonormální matici a horní trojúhelníkovou matici s naší bezplatnou online kalkulačkou rozkladu QR!
Zjistěte snadno přeponu pro všechny druhy trojúhelníků pomocí naší bezplatné matematické kalkulačky!
Spočítejte si snadno trigonometrické hodnoty Sin, Cos, Tan, Cot, Sec a Csc pomocí naší bezplatné online kalkulačky!
Zjistěte snadno pravou stranu a úhel trojúhelníku pomocí naší bezplatné online kalkulačky!
Vypočítejte přeponu, měření a poměr snadno pomocí naší kalkulačky trojúhelníku 45 45 90.
Vypočítejte snadno násobení matic pomocí naší bezplatné online matematické kalkulačky!
Vypočítejte si průměrný průměr čísel snadno pomocí naší bezplatné online matematické kalkulačky
Tento nástroj generuje skutečně náhodné číslo mezi libovolnými dvěma čísly.
Tato kalkulačka počítá chybovost pro průzkumy na základě velikosti a podílu vzorku. Umožňuje také nastavit požadovanou úroveň spolehlivosti.
Tento online nástroj počítá úhel mezi dvěma vektory a má všechny možné kombinace vektorů.
Tato kalkulačka vám pomůže najít LCM nebo LCD pro konkrétní sadu čísel.
Tato online kalkulačka vypočítá plochu tvaru měřenou ve stopách. Funguje se všemi tvary a měrnými jednotkami!
Toto je online kalkulačka, která umí vypočítat exponenty.
Tento online nástroj vypočítá zbytek dělení.
Spočítejte si snadno přímou úměru čísel pomocí naší bezplatné kalkulačky Pravidlo tří.
Kvadratické rovnice jsou jakákoli polynomiální algebra druhého stupně, která má v algebře následující tvar.
Tato kalkulačka součtového zápisu vám umožňuje rychle vypočítat součet nastaveného čísla, známého také jako Sigma. Proto se často nazývá sigma kalkulačka. Poskytuje vám také ukázku ze série, která má být součtem. Lze jej použít v jednoduchém režimu k výpočtu jednoduchého součtu pomocí dané sady čísel.
Toto je bezplatný online nástroj, který spočítá obvod různých tvarů.
Toto je kalkulačka, která vypočítá z-skóre souboru dat.
Tuto Fibonacciho kalkulačku lze použít k libovolnému výpočtu členů Fibonacciho posloupnosti.
Je to bezplatná kalkulačka, která vám pomůže najít objem libovolné kapsle.
Je to bezplatná kalkulačka, která vám pomůže najít objem různých tvarů.
Je to bezplatná kalkulačka, která vám pomůže najít objem jakéhokoli trojúhelníkového hranolu.
Je to bezplatná kalkulačka, která vám pomůže zjistit objem krabice.
Tato kalkulačka počítá objem kužele a lze ji použít k řešení školních problémů.
Jedná se o online nástroj, který spočítá objem libovolné krychle.
Jedná se o online nástroj, který spočítá objem válce.
Toto je online kalkulačka, která vám pomůže vypočítat dilataci měřítka objektu.
Kalkulátor indexu biodiverzity Shannon lze použít k výpočtu diverzity druhů ve společenství. Ekologové mohou využít Shannonův index diverzity k získání užitečných informací o stanovišti.
Použijte tuto kalkulačku Bayesova teorému online k určení pravděpodobnosti události, která je podmíněna jinou událostí. Tento výpočet bere v úvahu předchozí pravděpodobnost A, pravděpodobnosti podmíněné B a podmíněné A a podmíněné A.
Antilogová kalkulačka umožňuje vypočítat funkci inverzního logaritmu. Vypočítejte antilogaritmus pro libovolné číslo s jakýmkoli základem, ať už je to 10, přirozený antilog nebo jiné číslo.
Tento úžasný nástroj vám umožní vypočítat e na mocninu libovolného čísla, které si vyberete.
Tato kalkulačka vám ukáže, zda má číslo prvočíslo nebo je složené.
Kalkulačka exponenciálního růstu vypočítá konečnou cenu množství na základě jeho počátečních hodnot, rychlosti růstu a času.
Vypočítejte velikost vzorku na základě velikosti populace, úrovně spolehlivosti a meze chyby.
Tato online kalkulačka zobrazí inverzní log zadaného čísla a základu.
Kalkulačka Poissonova rozdělení vám umožní určit pravděpodobnost, že k události dojde několikrát během určitého časového rámce.
Tato kalkulačka vám pomůže najít násobící převrácenou hodnotu celého čísla, desetinného čísla, zlomku nebo smíšeného čísla.
Tato kalkulačka převádí testovací známky na procenta. Lze jej použít k rychlému výpočtu procenta jednoho nebo více známek (známek) testu a maximálního počtu známek.
Tuto kalkulačku lze použít k určení rozměrů obrázků při změně jejich velikosti.
Kalkulátor empirických pravidel, také známý jako "výpočet pravidel 68 95 99", je nástroj, který vám umožňuje určit rozsahy, které jsou buď 1 nebo 2 směrodatné odchylky nebo 3 směrodatné odchylky. Tato kalkulačka vám ukáže rozsahy, ve kterých je 68, 95 nebo 99,7 % normálně distribuovaných dat.
Tento neuvěřitelný nástroj vám umožní najít p-hodnotu. Pomocí testovací statistiky můžete určit, která p-hodnota je jednostranná a která oboustranná.
Je to bezplatná kalkulačka, která vám pomůže najít objem koule.
Tato online kalkulačka vám umožní vypočítat NPV (Čistá současná hodnota) investice. Výpočet je založen na počáteční investici a diskontní sazbě. Můžete také vypočítat vnitřní míru návratnosti (IRR), hrubé výnosy a čisté peněžní toky.
Pomocí této kalkulačky zjistěte, jak procentuální snížení o jakoukoli částku změní výsledek. Jednoduše zadejte původní hodnotu, procentuální pokles a novou hodnotu pro výpočet změny.
Náš intuitivní nástroj vám umožní vybrat si z různých tvarů a vypočítá jejich plochu během mrknutí oka.
Kalkulačka pravděpodobnosti vám umožní prozkoumat vztahy pravděpodobnosti mezi dvěma samostatnými událostmi. To vám umožní lépe porozumět tomu, jak spolu události souvisí, a díky tomu jsou předpovědi přesnější.
Použijte naši kalkulačku zlomků na desetinná místa ke snadnému převodu zlomků na desetinná místa a zpět!
Zjistěte faktory libovolného čísla pomocí naší kalkulačky faktorů
Převeďte zlomek na kalkulačku smíšených čísel pomocí našeho jednoduchého nástroje