Máy Tính Chuyển Vị Ma Trận
Máy tính chuyển vị ma trận này giúp bạn tìm phép chuyển vị cho bất kỳ ma trận nào.
Mục lục
Làm thế nào để sử dụng máy tính chuyển vị ma trận?
Chuyển vị ma trận là gì?

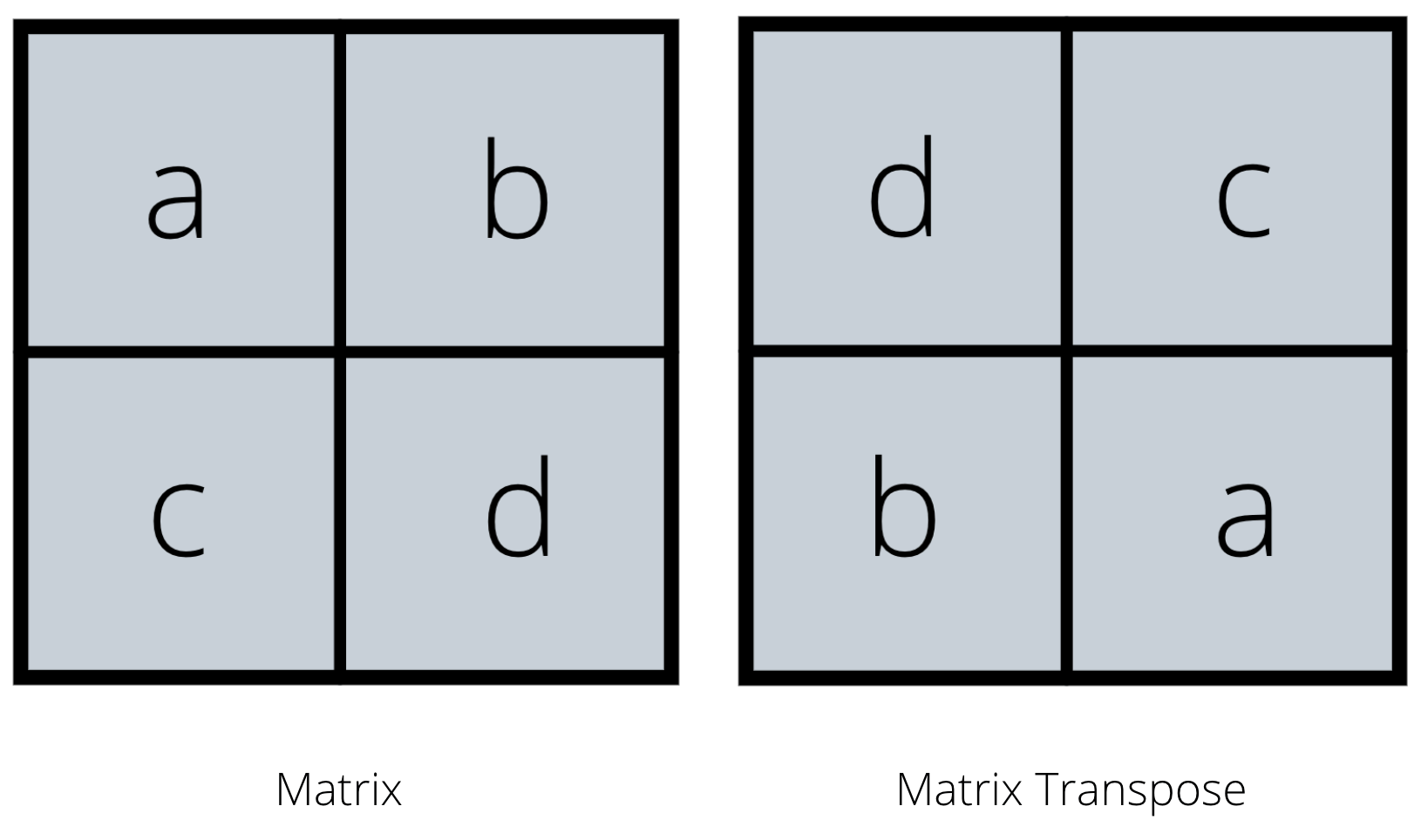
Làm thế nào để tính toán một ma trận chuyển vị theo cách thủ công?
Chuyển vị ma trận được sử dụng để làm gì?
Thuộc tính của chuyển vị
1) Chuyển vị của một bội số vô hướng
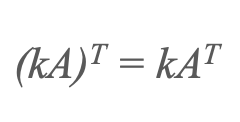
2) Chuyển đổi một tổng
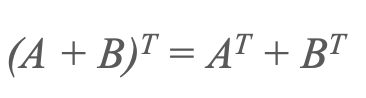
3) Chuyển vị của một sản phẩm
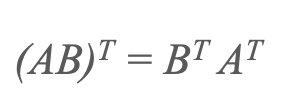

4) Chuyển vị của hoán vị
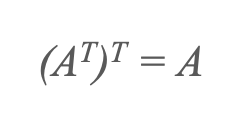
Các loại ma trận khác nhau
1) Ma trận hàng và cột

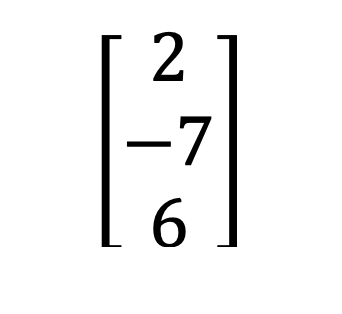
2) Ma trận hình chữ nhật & hình vuông
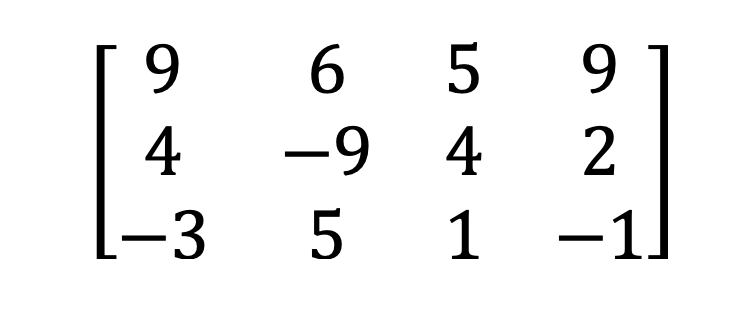
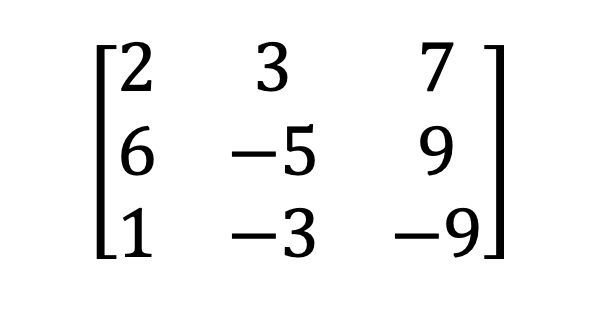
3) Ma trận số ít & không số ít
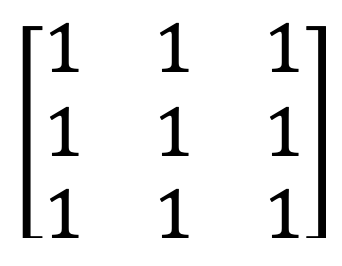
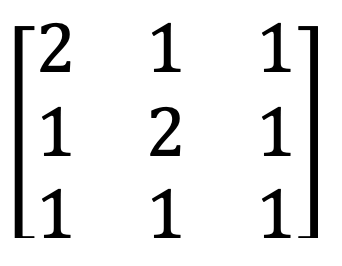
4) Ma trận nhận dạng
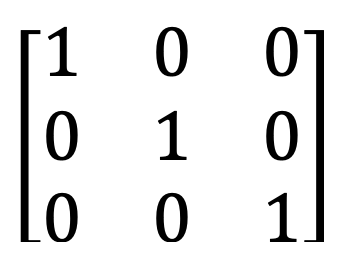
5) Ma trận của những cái
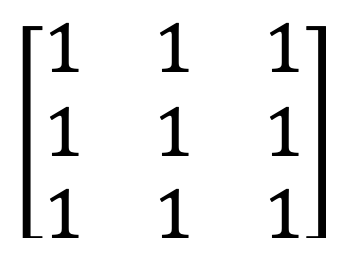
6) Ma trận 0
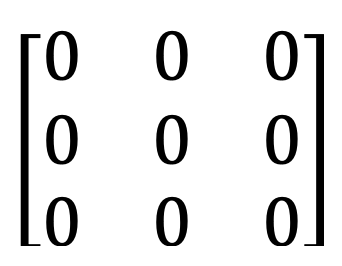
7) Ma trận đường chéo và ma trận vô hướng
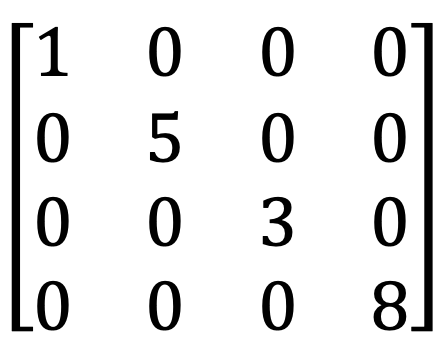

8) Ma trận tam giác trên và dưới

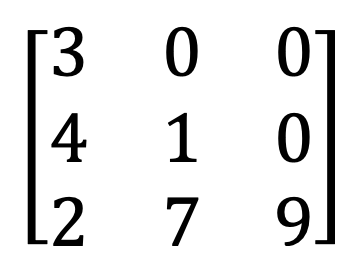
9) Ma trận đối xứng và xiên đối xứng
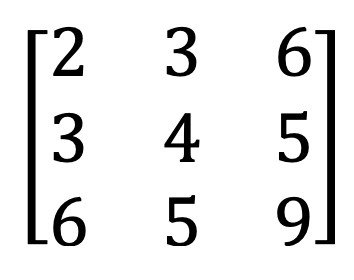
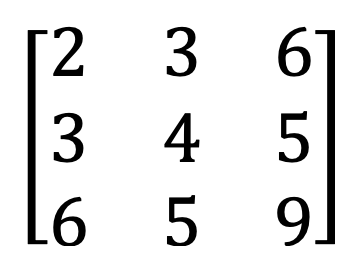
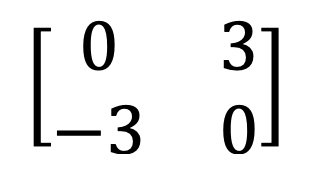
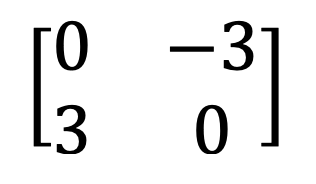
10) Ma trận boolean
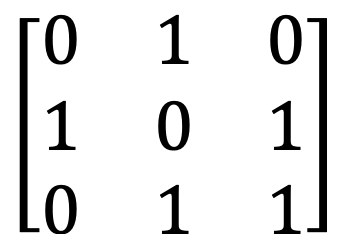
11) Ma trận ngẫu nhiên

12) Ma trận trực giao
Lịch sử chuyển vị

Máy Tính Chuyển Vị Ma Trận Tiếng Việt
Máy tính toán học khác
Máy tính tích chéo vectơ tìm tích chéo của hai vectơ trong không gian ba chiều.
Với máy tính tam giác 30 60 90 của chúng tôi, bạn có thể giải được tam giác vuông đặc biệt.
Công cụ tính giá trị kỳ vọng này giúp bạn tính giá trị kỳ vọng (còn gọi là giá trị trung bình) của tập biến đã cho với xác suất của chúng.
Máy tính khoa học này cung cấp các hàm toán học đơn giản và nâng cao trong một ứng dụng dễ sử dụng.
Máy tính miễn phí này cung cấp cho bạn độ lệch chuẩn, phương sai, giá trị trung bình và tổng của một tập dữ liệu nhất định.
Máy tính tỷ lệ phần trăm này là một máy tính trực tuyến miễn phí để tính toán tỷ lệ phần trăm. Tìm X% của Y là bao nhiêu?
Máy tính phân số miễn phí này có thể được sử dụng để tìm kết quả của phép cộng, trừ, nhân và chia hai phân số chung.
Tìm ra các phép đo chính xác cho công thức yêu thích của bạn với máy tính miễn phí này giúp chuyển đổi pound thành cốc một cách dễ dàng! Làm việc với cốc Hoa Kỳ và cốc Vương quốc Anh!
Sử dụng máy tính chu vi hình tròn miễn phí này để tính bán kính hình tròn, đường kính hình tròn, chu vi hình tròn và diện tích hình tròn.
Xác định góc tương đương của một góc cho trước bằng máy tính miễn phí này! Tìm thêm thông tin về công thức góc kép.
Máy tính miễn phí này tính toán số mũ và căn bậc hai, thứ ba trở lên. Công thức cũng có sẵn.
Dễ dàng tìm ra diện tích tam giác với máy tính diện tích tam giác miễn phí của chúng tôi! Bạn có thể tính toán với cơ sở và chiều cao, ba cạnh khác nhau và nhiều hơn nữa. Hoạt động với góc và radian!
Tìm ra các góc coterminal với máy tính góc coterminal của chúng tôi! Làm việc với độ và radian để tìm ra góc tọa độ âm và dương!
Dễ dàng tính toán các sản phẩm chấm toán học, tích vô hướng và các góc sản phẩm chấm cho các vectơ của bạn.
Dễ dàng tìm ra trung điểm của một đoạn thẳng hoặc một tam giác với máy tính trung điểm của chúng tôi! Trang này cũng sẽ dạy bạn công thức điểm giữa có giá trị!
Dễ dàng tìm ra số lượng chính xác các số liệu quan trọng trong số của bạn với công cụ số liệu quan trọng của chúng tôi!
Dễ dàng tìm ra độ dài của cung tròn bằng máy tính toán trực tuyến này!
Tính toán ước tính điểm một cách dễ dàng với công cụ trực tuyến miễn phí của chúng tôi!
Dễ dàng tính toán bất kỳ phần trăm tăng nào bằng máy tính trực tuyến miễn phí của chúng tôi!
Tính toán phần trăm chênh lệch ngay lập tức với máy tính phần trăm chênh lệch toán học của chúng tôi!
Máy tính trực tuyến miễn phí này tính toán nội suy tuyến tính và ngoại suy tuyến tính. Nó cũng cung cấp hệ số góc của phương trình tuyến tính.
Dễ dàng tìm ra ma trận chính quy và ma trận tam giác trên bằng máy tính phân rã QR trực tuyến miễn phí của chúng tôi!
Dễ dàng tìm ra cạnh huyền cho tất cả các loại tam giác bằng máy tính toán miễn phí của chúng tôi!
Dễ dàng tính toán các giá trị lượng giác Sin, Cos, Tan, Cot, Sec và Csc bằng máy tính trực tuyến miễn phí của chúng tôi!
Dễ dàng tìm ra cạnh và góc bên phải của một tam giác bằng máy tính trực tuyến miễn phí của chúng tôi!
Tính cạnh huyền, số đo và tỉ số dễ dàng với máy tính tam giác 45 45 90 của chúng tôi.
Tính toán các phép nhân ma trận một cách dễ dàng với máy tính toán học trực tuyến miễn phí của chúng tôi!
Tính toán trung bình cộng của các số một cách dễ dàng với máy tính toán học trực tuyến miễn phí của chúng tôi
Công cụ này tạo ra một số thực sự ngẫu nhiên giữa hai số bất kỳ.
Máy tính này tính toán biên độ sai số cho các cuộc khảo sát dựa trên kích thước và tỷ lệ mẫu. Nó cũng cho phép bạn thiết lập mức độ tin cậy mong muốn.
Công cụ trực tuyến này tính toán góc giữa hai vectơ và có tất cả các kết hợp vectơ có thể có.
Máy tính này sẽ giúp bạn tìm LCM hoặc LCD cho một bộ số cụ thể.
Máy tính trực tuyến này tính toán diện tích của một hình dạng được tính bằng feet. Hoạt động với tất cả các hình dạng và đơn vị đo lường!
Đây là một máy tính trực tuyến có thể tính toán số mũ.
Công cụ trực tuyến này tính toán phần còn lại của một phép chia.
Dễ dàng tính tỷ lệ trực tiếp của các số với máy tính Quy tắc ba miễn phí của chúng tôi.
Phương trình bậc hai là bất kỳ đại số đa thức bậc hai có dạng sau trong đại số.
Máy tính ký hiệu tổng này cho phép bạn nhanh chóng tính tổng của một tập hợp số, còn được gọi là Sigma. Do đó nó thường được gọi là máy tính sigma. Nó cũng cung cấp cho bạn một mẫu từ chuỗi thành một tổng. Nó có thể được sử dụng ở chế độ đơn giản để tính tổng đơn giản bằng cách sử dụng một bộ số nhất định.
Đây là một công cụ trực tuyến miễn phí sẽ tính chu vi của các hình dạng khác nhau.
Đây là một máy tính tính điểm z của một tập dữ liệu.
Máy tính Fibonacci này có thể được sử dụng để tính toán các số hạng tùy ý của dãy Fibonacci.
Nó là một máy tính miễn phí có thể giúp bạn tìm thể tích của bất kỳ viên nang nào.
Đây là một máy tính miễn phí có thể giúp bạn tìm khối lượng của các hình dạng khác nhau.
Đây là một máy tính miễn phí có thể giúp bạn tìm thể tích của bất kỳ hình lăng trụ tam giác nào.
Đây là một máy tính miễn phí có thể giúp bạn tìm thể tích của một chiếc hộp.
Máy tính này tính thể tích hình nón và có thể được sử dụng để giải các bài toán ở trường.
Đây là một công cụ trực tuyến sẽ tính toán thể tích của bất kỳ khối lập phương nào.
Đây là một công cụ trực tuyến sẽ tính toán thể tích của một hình trụ.
Đây là một máy tính trực tuyến sẽ giúp bạn tính toán độ giãn của hệ số tỷ lệ của một đối tượng.
Máy tính chỉ số đa dạng sinh học Shannon có thể được sử dụng để tính toán mức độ đa dạng của các loài trong một quần xã. Các nhà sinh thái học có thể sử dụng chỉ số đa dạng Shannon để có được thông tin hữu ích về môi trường sống.
Sử dụng máy tính định lý Bayes này trực tuyến để xác định xác suất của một sự kiện có điều kiện với một sự kiện khác. Tính toán này tính đến xác suất trước của A, xác suất B có điều kiện và A có điều kiện và A có điều kiện.
Máy tính antilog cho phép bạn tính hàm logarit nghịch đảo. Tính toán phản hàm số cho bất kỳ số nào với bất kỳ cơ số nào, cho dù đó là 10, phản hàm số tự nhiên hay một số khác.
Công cụ tuyệt vời này sẽ cho phép bạn tính e theo lũy thừa của bất kỳ số nào bạn chọn.
Máy tính này sẽ cho bạn biết liệu một số có là số nguyên tố hay là hợp số.
Máy tính tăng trưởng theo cấp số nhân tính toán giá cuối cùng của một số lượng dựa trên các giá trị ban đầu, tốc độ tăng trưởng và thời gian của nó.
Tính toán kích thước mẫu dựa trên quy mô dân số, mức độ tin cậy và biên độ sai số.
Máy tính trực tuyến này sẽ hiển thị nhật ký nghịch đảo của số và cơ số đã nhập.
Máy tính phân phối Poisson sẽ cho phép bạn xác định khả năng một sự kiện xảy ra một số lần trong một khung thời gian nhất định.
Máy tính này sẽ giúp bạn tìm nghịch đảo nhân của một số nguyên, một số thập phân, một phân số hoặc một hỗn số.
Máy tính này chuyển đổi điểm kiểm tra thành tỷ lệ phần trăm. Nó có thể được sử dụng để nhanh chóng tính toán tỷ lệ phần trăm của một hoặc nhiều điểm kiểm tra (điểm) và số điểm tối đa.
Máy tính này có thể được sử dụng để xác định kích thước của hình ảnh khi bạn thay đổi kích thước của chúng.
Máy tính quy tắc thực nghiệm, còn được gọi là "phép tính quy tắc 68 95 99", là một công cụ cho phép bạn xác định phạm vi là 1 hoặc 2 độ lệch chuẩn hoặc 3 độ lệch chuẩn. Máy tính này sẽ hiển thị cho bạn phạm vi tương ứng là 68, 95 hoặc 99,7% dữ liệu được phân phối bình thường.
Công cụ đáng kinh ngạc này sẽ cho phép bạn tìm giá trị p. Bạn có thể sử dụng thống kê thử nghiệm để xác định giá trị p nào là một phía và giá trị nào là hai phía.
Đây là một máy tính miễn phí có thể giúp bạn tìm thể tích của một hình cầu.
Máy tính trực tuyến này sẽ cho phép bạn tính NPV (Giá trị hiện tại ròng) của một khoản đầu tư. Việc tính toán dựa trên vốn đầu tư ban đầu và tỷ lệ chiết khấu. Bạn cũng có thể tính Tỷ lệ hoàn vốn nội bộ (IRR), lợi nhuận gộp và dòng tiền ròng.
Sử dụng máy tính này để tìm hiểu xem việc giảm tỷ lệ phần trăm của bất kỳ số tiền nào sẽ thay đổi kết quả như thế nào. Chỉ cần nhập giá trị ban đầu, phần trăm giảm và giá trị mới để tính toán thay đổi.
Công cụ trực quan của chúng tôi cho phép bạn chọn từ các hình dạng khác nhau và tính toán diện tích của chúng trong nháy mắt.
Máy tính xác suất cho phép bạn khám phá các mối quan hệ về khả năng xảy ra giữa hai sự kiện riêng biệt. Điều này cho phép bạn hiểu rõ hơn về mối liên hệ giữa các sự kiện và từ đó đưa ra dự đoán chính xác hơn.
Sử dụng máy tính phân số thành số thập phân của chúng tôi để dễ dàng chuyển đổi phân số thành số thập phân và ngược lại!
Tìm ra các yếu tố của bất kỳ số nào với máy tính yếu tố của chúng tôi
Chuyển đổi một phân số thành một máy tính hỗn số bằng công cụ đơn giản của chúng tôi