Matrix Transpose Calculator
This matrix transpose calculator helps you to find a transpose for any matrix.
Table of contents
How to use matrix transpose calculator?
What is a matrix transpose?

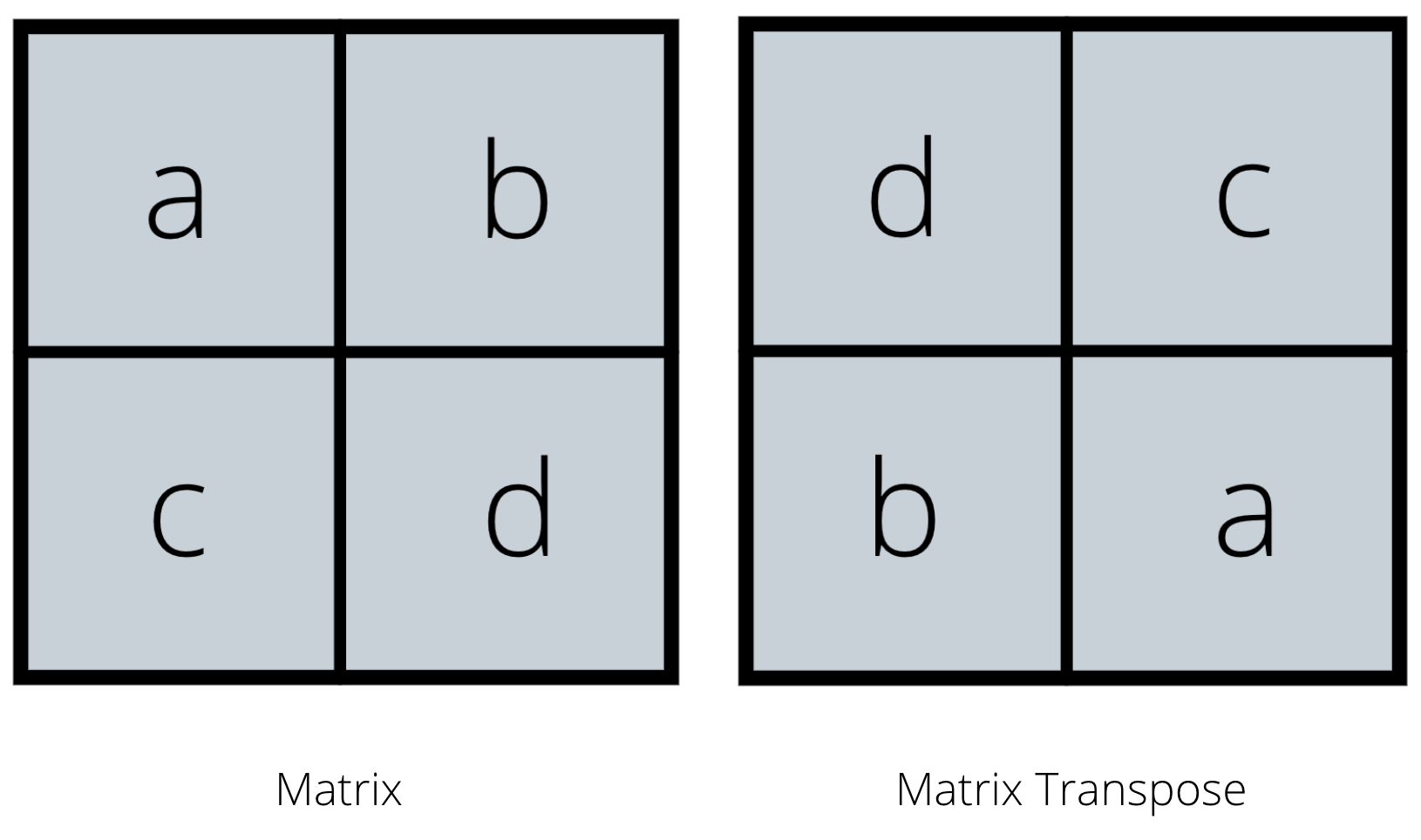
How to manually calculate a matrix transpose?
What is the matrix transpose used for?
Properties of transposes
1) Transpose of a scalar multiple
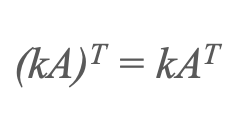
2) Transpose of a sum
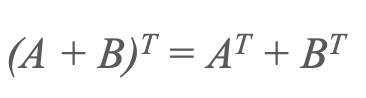
3) Transpose of a product
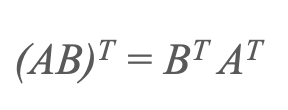

4) Transpose of the transpose
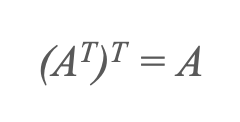
Different types of matrices
1) Row and column matrix

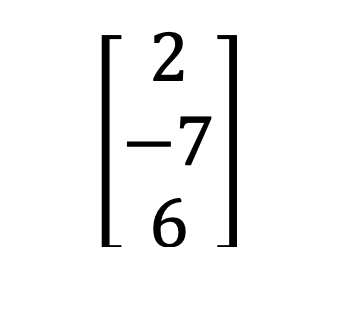
2) Rectangular & square matrix
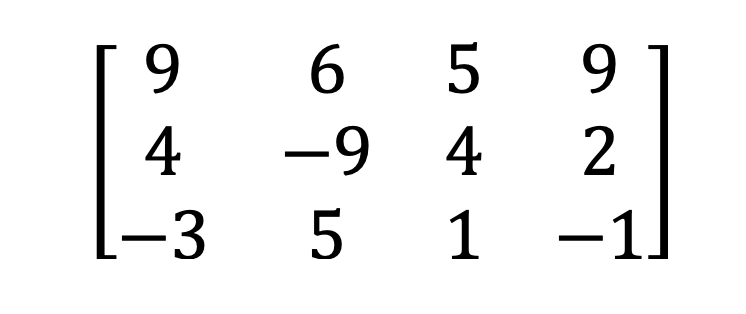
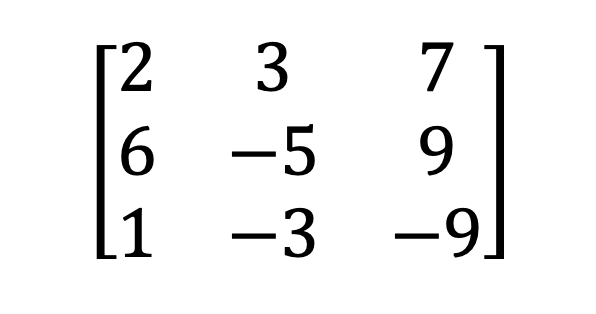
3) Singular & non-singular matrix
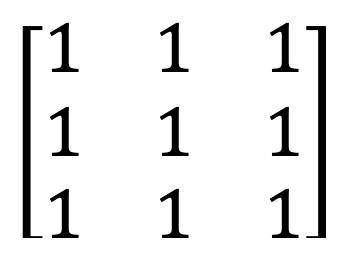
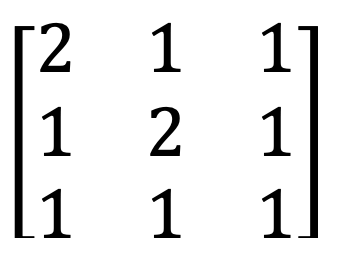
4) Identity matrix
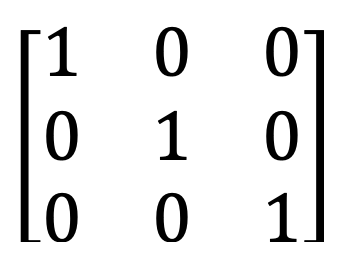
5) Matrix of ones
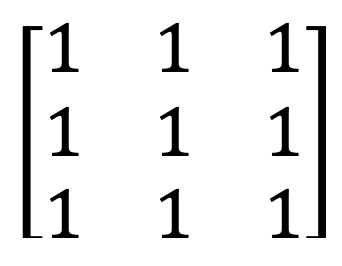
6) Zero matrix
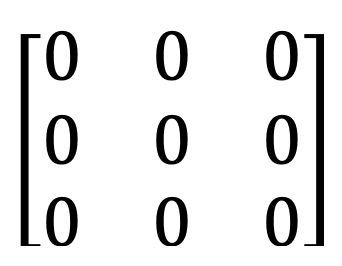
7) Diagonal matrix and scalar matrix
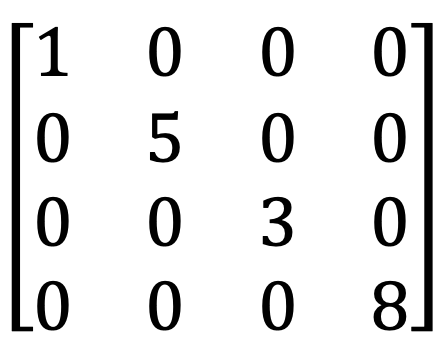

8)Upper & lower triangular matrix

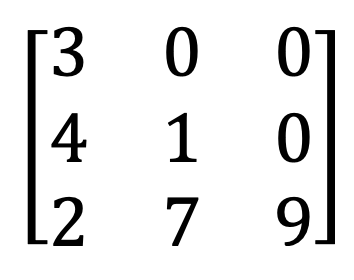
9) Symmetric and skew-symmetric matrix
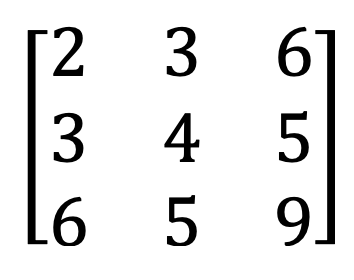
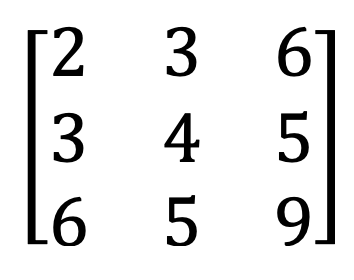
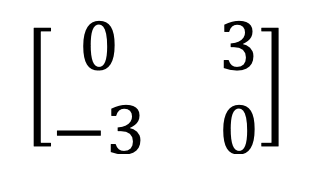
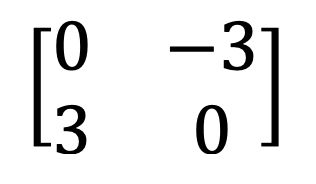
10) Boolean matrix
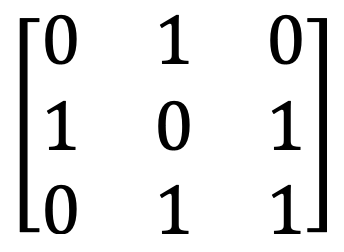
11) Stochastic matrices

12) Orthogonal matrix
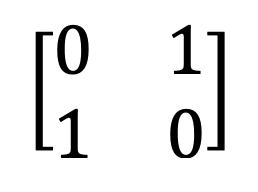
History of transpose

Matrix Transpose Calculator English
Other mathematical calculators
Vector cross product calculator finds the cross product of two vectors in a three-dimensional space.
With our 30 60 90 triangle calculator you can solve the special right triangle.
This expected value calculator helps you to calculate an expected value (also called mean) of the given variable set with their probabilities.
This scientific calculator provides simple and advanced mathematical functions in an easy-to-use app.
This free calculator gives you the standard deviation, variance, mean, and sum of a given data set.
This percentage calculator is a free online calculator to calculate percentages. Find out what is X % of Y?
This free fraction calculator can be used to find the result for adding, subtracting, multiplying, and dividing two common fractions.
Find out correct measurements for your favourite recipe with this free calculator converts pounds to cups easily! Works with US cups and UK cups!
Use this free circle circumference calculator to calculate circle radius, circle diameter, circle circumference, and circle area.
Determine the double angle equivalent of a given angle with this free calculator! Find more information about the double angle formula.
This free calculator calculates the second, third and higher exponents and roots. Formula is also available.
Find out area of triangle easily with our free triangle area calculator! You can calculate with base and height, three different sides and many more. Works with angles and radians!
Find out coterminal angles with our coterminal angle calculator! Works with degrees and radians to find out positive and negative coterminal angles!
Calculate mathematical dot products, scalar products and dot product angles easily for your vectors.
Find out midpoints for a line or a triangle easily with our midpoint calculator! This page will also teach you valuable midpoint formula!
Find out the correct amount of significant figures in your number easily with our significant figure tool!
Find out easily length of a circle's arc with this online math calculator!
Calculate point estimate easily with our free online tool!
Calculate any percentage increase easily with our free online calculator!
Calculate percentage difference instantly with our mathematical percentage difference calculator!
This free online calculator calculates the linear interpolation and the linear extrapolation. It also provides the slope of the linear equation.
Find out orthonormal matrix and upper triangular matrix easily with our free online QR decomposition calculator!
Find out hypotenuse for all kinds of triangles easily with our free math calculator!
Calculate easily trigonometric values Sin, Cos, Tan, Cot, Sec and Csc with our free online calculator!
FInd out easily right side and angle of an triangle with our free online calculator!
Calculate hypotenuse, measurements and ratio easily with our 45 45 90 triangle calculator.
Calculate matrix multiplications easily with our free online math calculator!
Calculate mean average of numbers easily with our free online math calculator
This tool generates a truly random number between any two numbers.
This calculator calculates the margin of error for surveys based on sample size and proportion. It also allows you to set the desired level of confidence.
This online tool calculates the angle between two vectors and has all the possible vector combinations.
This calculator will help you find the LCM or LCD for a particular set of numbers.
This online calculator calculates the area of a shape measured in feet. Works with all shapes and measurement units!
This is an online calculator that can calculate exponents.
This online tool calculates the remainder of a division.
Calculate easily direct proportion of numbers with our free Rule of Three calculator.
Quadratic equations are any polynomial algebra of the second degree having the following form in algebra.
This summation notation calculator allows you to quickly calculate the summation of a set number, also known as Sigma. Therefore it is often called a sigma calculator. It also gives you a sample from the series to be a sum. It can be used in simple mode to calculate a simple sum using a given set of numbers.
This is a free online tool that will calculator the perimeter of different shapes.
This is a calculator that calculates the z-score of a data set.
This Fibonacci calculator can be used to calculate the terms arbitrarily of the Fibonacci sequence.
It is a free calculator that can help you find the volume of any capsule.
It is a free calculator that can help you find the volume of different shapes.
It is a free calculator that can help you find the volume of any triangular prism.
It is a free calculator that can help you find the volume of a box.
This calculator calculates cone volume and can be used to solve school problems.
This is an online tool that will calculate the volume of any cube.
This is an online tool that will calculate the volume of a cylinder.
This is an online calculator that will help you calculate the scale factor dilation of an object.
The Shannon biodiversity index calculator can be used to calculate the diversity of species in a community. Ecologists can use the Shannon diversity index to gain useful information about habitat.
Use this Bayes theorem calculator online to determine the probability of an event that is conditional on another. This calculation takes into account the prior probability of A, the probabilities B conditional and A conditional, and A conditional.
The antilog calculator allows you to calculate the inverse logarithm function. Calculate the antilogarithm for any number with any base, whether it's 10, natural antilog, or another number.
This amazing tool will allow you to compute e to the power of any number you choose.
This calculator will show you whether a number has a prime number or if it is a composite.
The exponential Growth Calculator calculates the final price of a quantity based on its initial values, rate of growth, and time.
Calculate sample size based on the population size, confidence level, and margin of error.
This online calculator will display the inverse log of the number and the base entered.
The Poisson distribution calculator will allow you to determine the likelihood of an event occurring a number of times during a certain time frame.
This calculator will help you find the multiplicative inverse of an integer, a decimal, a fraction, or a mixed number.
This calculator converts test marks to percentages. It can be used to quickly calculate the percentage of one or more test grades (marks), and the maximum number of marks.
This calculator can be used to determine the dimensions of images when you resize them.
The empirical rule calculator, also known as a "68 95 99 rule calculation", is a tool that allows you to determine the ranges that are either 1 or 2 standard deviations or 3 standard deviations. This calculator will show you the ranges in which 68, 95, or 99.7% of normally distributed data, respectively.
This incredible tool will allow you to find the p-value. You can use test statistics to determine which p-value is one-sided and which is two-sided.
It is a free calculator that can help you find the volume of a sphere.
This online calculator will allow you to calculate the NPV (Net Present Value) of an investment. The calculation is based on the initial investment and the discount rate. You can also calculate Internal Rates of Return (IRR), gross returns, and net cash flows.
Use this calculator to find out how a percentage decrease by any amount will change the result. Simply enter the original value, the percentage decrease, and the new value to calculate the change.
Our intuitive tool lets you choose from different shapes and calculates their area in the blink of an eye.
The probability calculator lets you explore the relationships of likelihood between two separate events. This allows you to get a better understanding of how events are related, and thereby makes predictions more accurate.
Use our fraction to decimal calculator to easily convert fractions to decimals and back again!
Find out the factors of any number with our factor calculator
Convert a fraction to a mixed number calculator using our simple tool