Matrix Köçürmə Kalkulyatoru
Bu matris köçürmə kalkulyatoru, hər hansı bir matris üçün bir köçürmə tapmağa kömək edir.
Mündəricat
Matris köçürmə kalkulyatorundan necə istifadə etmək olar?
Matris köçürmə nədir?

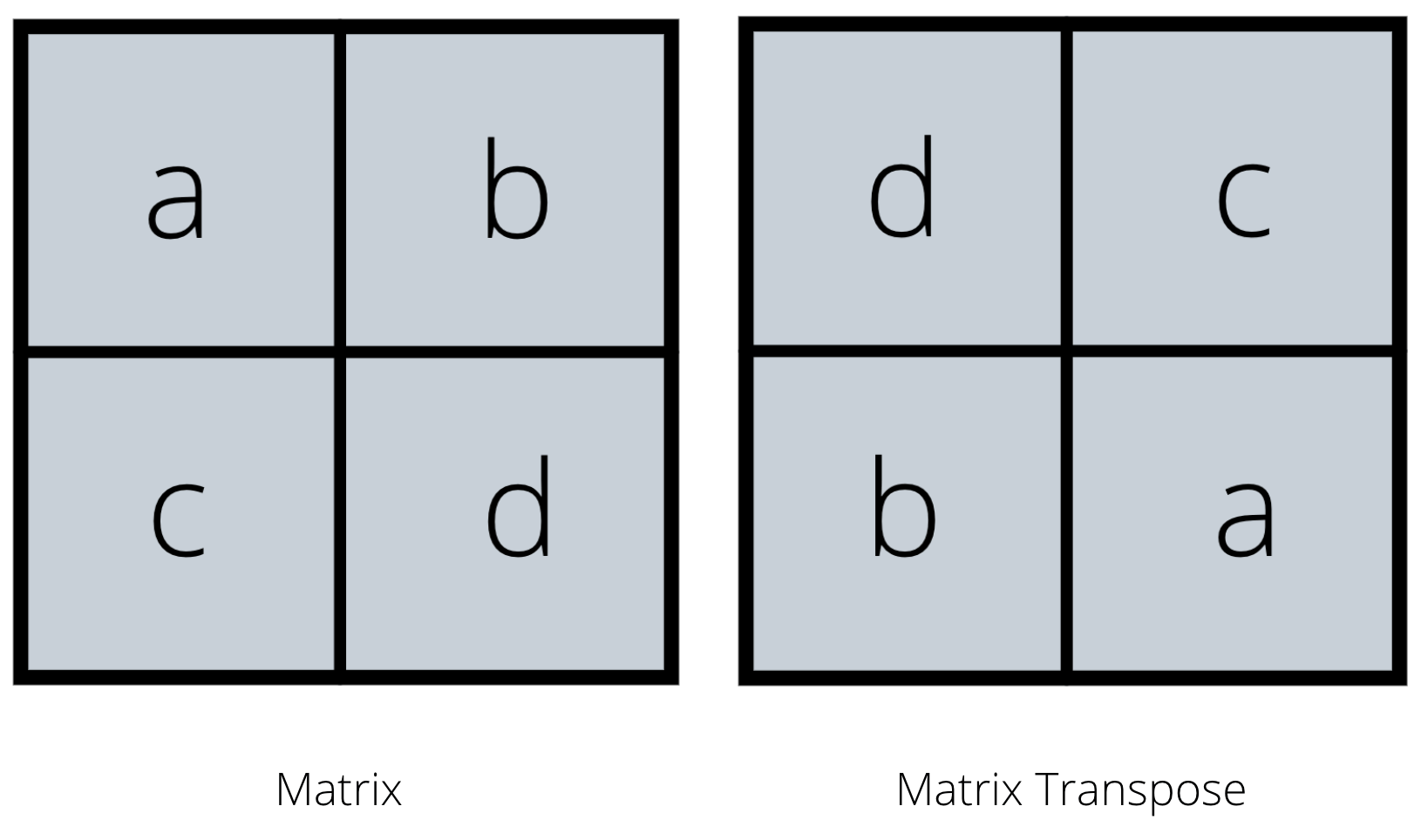
Bir matris köçürməsini əllə necə hesablamaq olar?
Matris transpozisiyası nə üçün istifadə olunur?
Transpozisiyanın xüsusiyyətləri
1) Skalyar çoxluğun köçürülməsi
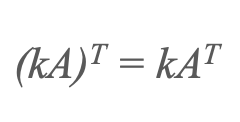
2) Bir məbləğin köçürülməsi
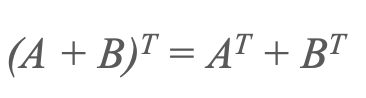
3) Məhsulun köçürülməsi
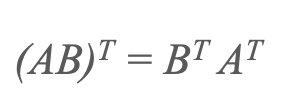

4) Transpozisiyanın köçürülməsi
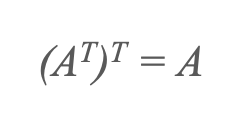
Müxtəlif növ matrislər
1) Satır və sütun matrisi

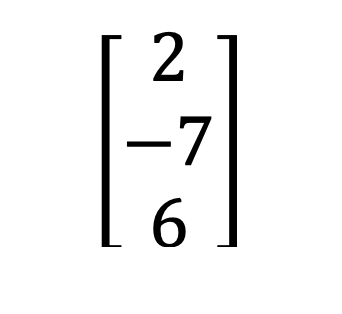
2) Düzbucaqlı və kvadrat matris
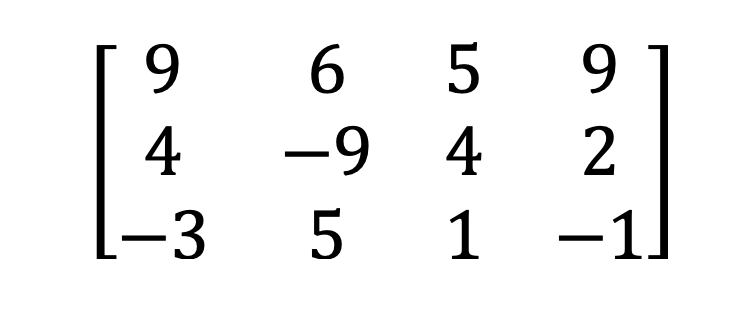
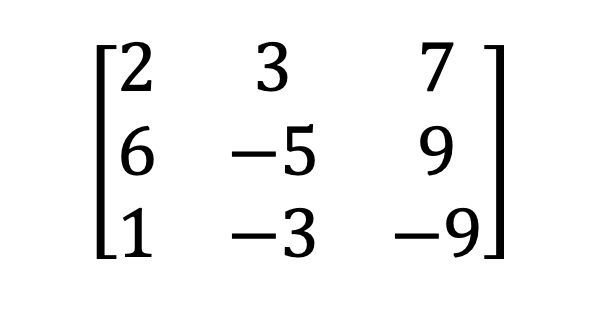
3) Tək və tək olmayan matris
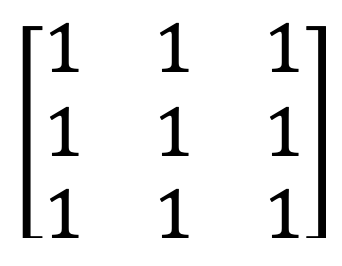
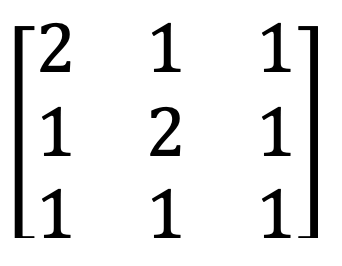
4) Şəxsiyyət matrisi
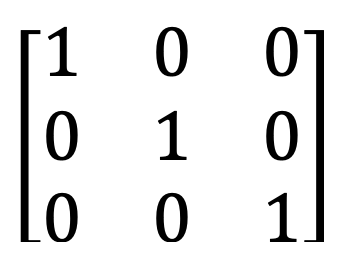
5) Birlərin matrisi
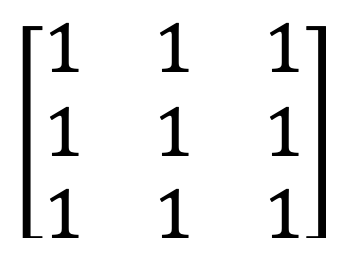
6) Sıfır matris
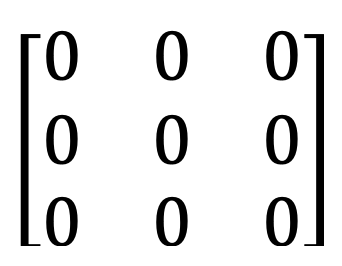
7) Çapraz matris və skalyar matris
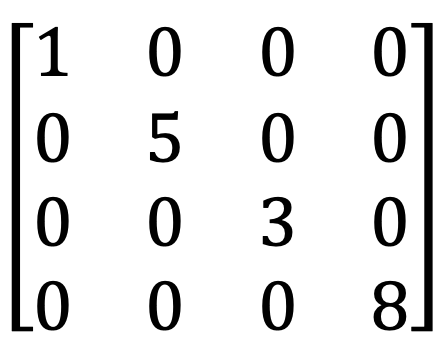

8) Yuxarı və aşağı üçbucaqlı matris

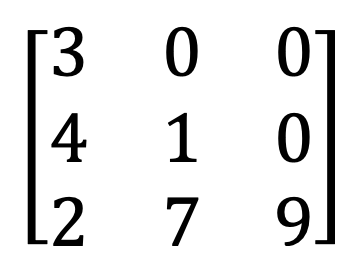
9) Simmetrik və əyri-simmetrik matris
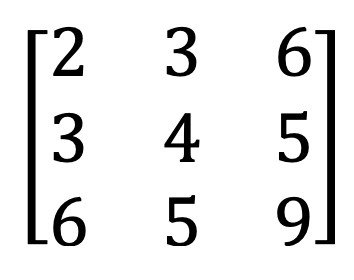
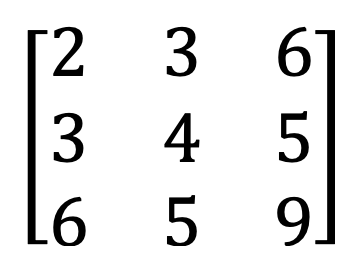
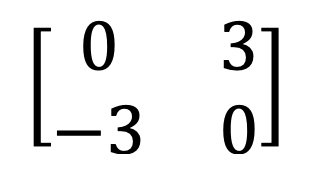
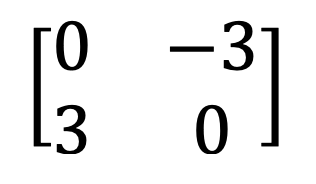
10) Boolean matris
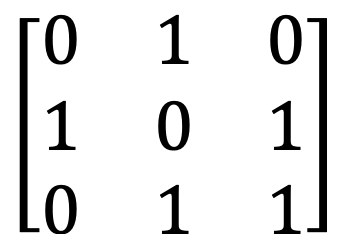
11) Stokastik matrislər

12) Ortogonal matris
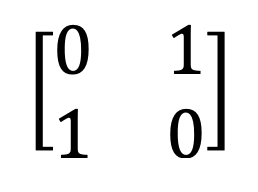
Transpozisiyanın tarixi

Matrix Köçürmə Kalkulyatoru Azərbaycan
Digər riyazi hesablayıcılar
Vector cross məhsul kalkulyatoru üçölçülü bir fəzada iki vektorun çarpaz məhsulunu tapır.
30 60 90 üçbucaq kalkulyatorumuzla xüsusi düzbucaqlı üçbucağı həll edə bilərsiniz.
Bu gözlənilən dəyər kalkulyatoru, verilən dəyişənin ehtimalları ilə birlikdə gözlənilən dəyəri (orta da deyilir) hesablamağa kömək edir.
Bu elmi kalkulyator, istifadəsi asan bir tətbiqdə sadə və inkişaf etmiş riyazi funksiyaları təmin edir.
Bu pulsuz kalkulyator sizə verilən məlumat dəstinin standart sapmasını, variasiyasını, ortasını və cəmini verir.
Bu faiz kalkulyatoru, faizləri hesablamaq üçün pulsuz bir onlayn kalkulyatordur. Y-nin X% -i nədir?
Bu pulsuz hissə kalkulyatoru, iki ümumi fraksiyanı əlavə etmək, çıxmaq, vurmaq və bölmək üçün nəticəni tapmaq üçün istifadə edilə bilər.
Bu pulsuz kalkulyatorla funtu asanlıqla fincanlara çevirərək sevimli reseptiniz üçün düzgün ölçüləri tapın! ABŞ kubokları və Böyük Britaniya kubokları ilə işləyir!
Dairə radiusunu, dairə diametrini, dairə çevrəsini və dairə sahəsini hesablamaq üçün bu pulsuz dairə çevrəsi kalkulyatorundan istifadə edin.
Bu pulsuz kalkulyatorla müəyyən bir açının ikiqat bucaq ekvivalentini təyin edin! Cüt bucaq formulu haqqında daha çox məlumat əldə edin.
Bu pulsuz kalkulyator ikinci, üçüncü və daha yüksək göstəriciləri və kökləri hesablayır. Formula da mövcuddur.
Pulsuz üçbucaq sahə kalkulyatorumuzla üçbucağın sahəsini asanlıqla tapın! Baza və hündürlük, üç fərqli tərəf və daha çoxu ilə hesablaya bilərsiniz. Açılar və radianlarla işləyir!
Koterminal bucaq kalkulyatorumuzla koterminal açıları öyrənin! Müsbət və mənfi koterminal açıları öyrənmək üçün dərəcə və radianlarla işləyir!
Vektorlarınız üçün riyazi nöqtə məhsullarını, skaler məhsullarını və nöqtə məhsul açılarını asanlıqla hesablayın.
Orta xətt kalkulyatorumuzla bir xətt və ya üçbucağın orta nöqtələrini asanlıqla tapın! Bu səhifə sizə dəyərli orta nöqtə formulunu da öyrədəcək!
Əhəmiyyətli rəqəm vasitəmizlə nömrənizdəki doğru rəqəmlərin miqdarını asanlıqla tapın!
Bu onlayn riyaziyyat kalkulyatoru ilə dairənin qövsünün uzunluğunu asanlıqla tapın!
Pulsuz onlayn vasitəmizlə asanlıqla xal hesablamasını hesablayın!
Pulsuz onlayn kalkulyatorumuzla istənilən faiz artımını asanlıqla hesablayın!
Riyazi faiz fərqi kalkulyatorumuzla faiz fərqini dərhal hesablayın!
Bu pulsuz onlayn kalkulyator xətti interpolasiyanı və xətti ekstrapolyasiyanı hesablayır. Həm də xətti tənliyin yamacını təmin edir.
Pulsuz onlayn QR parçalanma kalkulyatorumuzla ortonormal matris və yuxarı üçbucaq matrisini asanlıqla tapın!
Pulsuz riyaziyyat kalkulyatorumuzla hər cür üçbucaqlar üçün hipotenuzanı asanlıqla tapın!
Pulsuz onlayn kalkulyatorumuzla Sin, Cos, Tan, Cot, Sec və Csc triqonometrik dəyərlərini asanlıqla hesablayın!
Pulsuz onlayn kalkulyatorumuzla üçbucağın sağ tərəfini və bucağını asanlıqla tapın!
45 45 90 üçbucaq kalkulyatorumuzla hipotenuzanı, ölçmələri və nisbəti asanlıqla hesablayın.
Pulsuz onlayn riyaziyyat kalkulyatorumuzla matris vurmalarını asanlıqla hesablayın!
Pulsuz onlayn riyaziyyat kalkulyatorumuzla asanlıqla rəqəmlərin orta ortalamasını hesablayın
Bu alət hər hansı iki ədəd arasında həqiqətən təsadüfi bir ədəd yaradır.
Bu kalkulyator nümunənin ölçüsünə və nisbətinə əsasən sorğular üçün xəta marjasını hesablayır. O, həmçinin istədiyiniz güvən səviyyəsini təyin etməyə imkan verir.
Bu onlayn alət iki vektor arasındakı bucağı hesablayır və bütün mümkün vektor birləşmələrinə malikdir.
Bu kalkulyator sizə müəyyən ədədlər dəsti üçün LCM və ya LCD tapmağa kömək edəcək.
Bu onlayn kalkulyator futla ölçülən formanın sahəsini hesablayır. Bütün formalar və ölçü vahidləri ilə işləyir!
Bu eksponentləri hesablaya bilən onlayn kalkulyatordur.
Bu onlayn alət bölmənin qalan hissəsini hesablayır.
Pulsuz Rule of Three kalkulyatorumuzla nömrələrin birbaşa nisbətini asanlıqla hesablayın.
Kvadrat tənliklər cəbrdə aşağıdakı formaya malik ikinci dərəcəli hər hansı çoxhədli cəbrdir.
Bu cəmləmə notasiyası kalkulyatoru, Sigma kimi tanınan dəst nömrəsinin cəmini tez hesablamağa imkan verir. Buna görə də onu tez-tez siqma kalkulyatoru adlandırırlar. O, həmçinin cəmi olmaq üçün seriyadan bir nümunə verir. Verilmiş ədədlər toplusundan istifadə edərək sadə məbləği hesablamaq üçün sadə rejimdə istifadə edilə bilər.
Bu, müxtəlif formaların perimetrini hesablayacaq pulsuz onlayn vasitədir.
Bu, məlumat dəstinin z-hesabını hesablayan kalkulyatordur.
Bu Fibonacci kalkulyatoru Fibonacci ardıcıllığının şərtlərini özbaşına hesablamaq üçün istifadə edilə bilər.
Bu, istənilən kapsulun həcmini tapmaqda sizə kömək edə biləcək pulsuz kalkulyatordur.
Bu, müxtəlif formaların həcmini tapmaqda sizə kömək edə biləcək pulsuz kalkulyatordur.
Bu, istənilən üçbucaqlı prizmanın həcmini tapmaqda sizə kömək edə biləcək pulsuz kalkulyatordur.
Bu qutunun həcmini tapmaqda sizə kömək edə biləcək pulsuz kalkulyatordur.
Bu kalkulyator konus həcmini hesablayır və məktəb problemlərini həll etmək üçün istifadə edilə bilər.
Bu, istənilən kubun həcmini hesablayacaq onlayn bir vasitədir.
Bu, silindrin həcmini hesablayacaq onlayn bir vasitədir.
Bu, obyektin miqyası amilinin genişlənməsini hesablamağa kömək edəcək onlayn kalkulyatordur.
Şannon biomüxtəliflik indeksi kalkulyatoru icmadakı növlərin müxtəlifliyini hesablamaq üçün istifadə edilə bilər. Ekoloqlar yaşayış yeri haqqında faydalı məlumat əldə etmək üçün Şennon müxtəliflik indeksindən istifadə edə bilərlər.
Bu Bayes teoreminin onlayn kalkulyatorundan başqa bir hadisəyə şərti olan hadisənin ehtimalını təyin etmək üçün istifadə edin. Bu hesablamada A-nın əvvəlki ehtimalı, B şərti və A şərti ehtimalları və A şərti nəzərə alınır.
Antiloq kalkulyatoru tərs loqarifm funksiyasını hesablamağa imkan verir. İstənilən əsası olan istənilən ədəd üçün antiloqarifmi hesablayın, istər 10, istər təbii antiloq və ya başqa bir rəqəm.
Bu heyrətamiz alət sizə seçdiyiniz istənilən ədədin gücünə e-ni hesablamağa imkan verəcək.
Bu kalkulyator sizə nömrənin sadə və ya mürəkkəb olduğunu göstərəcək.
Eksponensial Artım Kalkulyatoru kəmiyyətin son qiymətini onun ilkin dəyərlərinə, artım sürətinə və vaxta əsasən hesablayır.
Nümunə ölçüsünü, etimad səviyyəsini və səhv həddi əsasında hesablayın.
Bu onlayn kalkulyator nömrənin və daxil edilmiş bazanın tərs jurnalını göstərəcək.
Poisson paylama kalkulyatoru sizə müəyyən vaxt çərçivəsində bir neçə dəfə baş verən hadisənin baş vermə ehtimalını müəyyən etməyə imkan verəcək.
Bu kalkulyator sizə tam ədədin, ondalığın, kəsrin və ya qarışıq ədədin çarpan tərsini tapmağa kömək edəcək.
Bu kalkulyator test işarələrini faizlərə çevirir. Bir və ya daha çox test qiymətlərinin (qiymətlərinin) faizini və maksimum qiymət sayını tez hesablamaq üçün istifadə edilə bilər.
Bu kalkulyator şəkillərin ölçüsünü dəyişdikdə onların ölçülərini müəyyən etmək üçün istifadə edilə bilər.
"68 95 99 qayda hesablaması" kimi tanınan empirik qayda kalkulyatoru 1 və ya 2 standart sapma və ya 3 standart sapma olan diapazonları müəyyən etməyə imkan verən alətdir. Bu kalkulyator sizə normal paylanmış məlumatların müvafiq olaraq 68, 95 və ya 99,7%-nin olduğu diapazonları göstərəcək.
Bu inanılmaz alət sizə p-dəyərini tapmağa imkan verəcək. Hansı p-dəyərinin birtərəfli və hansının ikitərəfli olduğunu müəyyən etmək üçün test statistikasından istifadə edə bilərsiniz.
Bu, sferanın həcmini tapmağa kömək edən pulsuz kalkulyatordur.
Bu onlayn kalkulyator sizə investisiyanın NPV-ni (Net Present Value) hesablamağa imkan verəcək. Hesablama ilkin investisiyaya və uçot dərəcəsinə əsaslanır. Siz həmçinin Daxili Gəlir dərəcələrini (IRR), ümumi gəlirləri və xalis pul vəsaitlərinin hərəkətini hesablaya bilərsiniz.
İstənilən məbləğin faiz azalmasının nəticəni necə dəyişəcəyini öyrənmək üçün bu kalkulyatordan istifadə edin. Dəyişikliyi hesablamaq üçün sadəcə olaraq orijinal dəyəri, faiz azalmasını və yeni dəyəri daxil edin.
Bizim intuitiv alətimiz sizə müxtəlif formalar arasından seçim etməyə və onların sahəsini bir göz qırpımında hesablamağa imkan verir.
Ehtimal kalkulyatoru iki ayrı hadisə arasında ehtimal əlaqələrini tədqiq etməyə imkan verir. Bu, hadisələrin necə əlaqəli olduğunu daha yaxşı başa düşməyə imkan verir və bununla da proqnozları daha dəqiq edir.
Fraksiyaları asanlıqla ondalığa çevirmək və yenidən geriyə çevirmək üçün kəsrdən decimal kalkulyatorumuzdan istifadə edin!
Faktor kalkulyatorumuzla istənilən ədədin faktorlarını tapın
Sadə alətimizdən istifadə edərək kəsri qarışıq ədədlərin kalkulyatoruna çevirin