目录
| ◦这个计算器怎么用? |
| ◦什么是标准差公式? |
| ◦人口标准差 |
| ◦样本标准差 |
| ◦未校正样本标准偏差 |
| ◦修正样本标准偏差 |
| ◦无偏样本标准差 |
| ◦标准差的应用 |
| ◦参考 |
这个计算器怎么用?
什么是标准差公式?
人口标准差
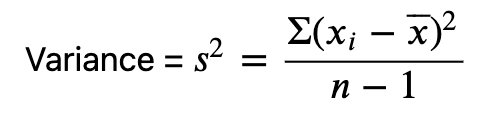

样本标准差
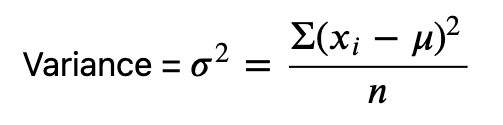
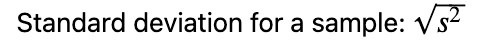
未校正样本标准偏差
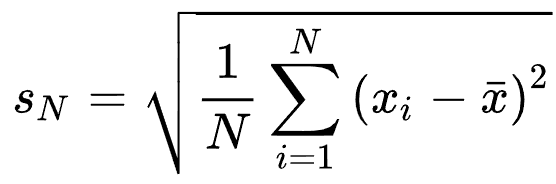
修正样本标准偏差
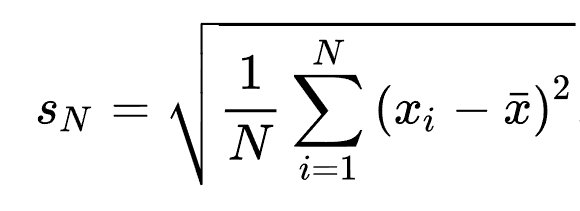
无偏样本标准差
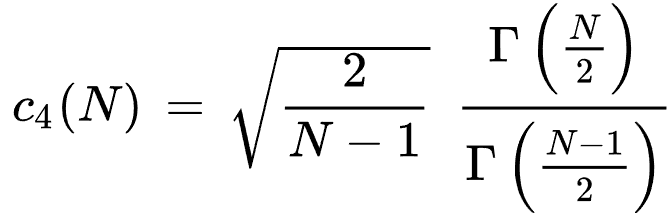
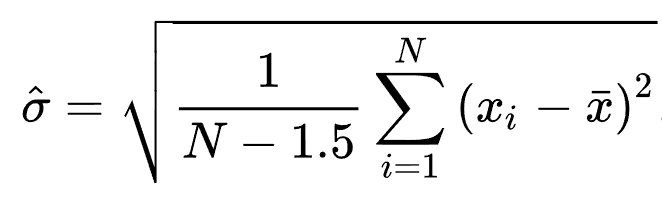
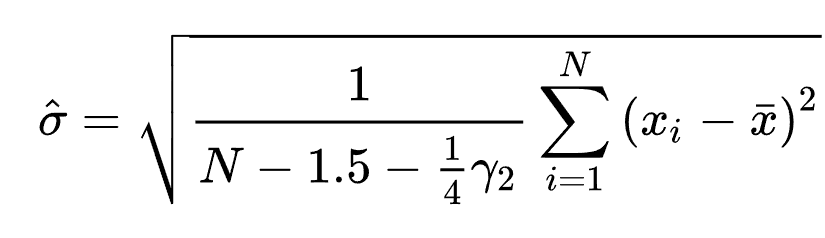
标准差的应用
参考

标准差计算器 普通话
其他数学计算器
向量叉积计算器在三维空间中找到两个向量的叉积。
使用我们的 30 60 90 三角形计算器,您可以求解特殊的直角三角形。
此期望值计算器可帮助您计算给定变量集及其概率的期望值(也称为平均值)。
这个科学计算器在一个易于使用的应用程序中提供了简单和高级的数学函数。
这个百分比计算器是一个免费的在线计算器来计算百分比。找出什么是 Y 的 X %?
这个免费的分数计算器可用于计算两个常见分数的加、减、乘和除结果。
使用这个免费的计算器为您最喜欢的食谱找出正确的测量值,轻松将磅转换为杯子!适用于美国杯和英国杯!
使用这个免费的圆周长计算器来计算圆半径、圆直径、圆周长和圆面积。
使用此免费计算器确定给定角度的双角等效值!查找有关双角公式的更多信息。
这个免费的计算器计算第二、第三和更高的指数和根。公式也可用。
使用我们的免费三角形面积计算器轻松计算三角形面积!您可以计算底和高、三个不同的边等等。适用于角度和弧度!
使用我们的共端角计算器找出共端角!使用度数和弧度来找出正负共端角!
轻松计算向量的数学点积、标量积和点积角度。
使用我们的中点计算器轻松找出直线或三角形的中点!本页还会教你宝贵的中点公式!
使用我们的有效数字工具轻松找出数字中正确数量的有效数字!
使用此在线数学计算器轻松找出圆弧的长度!
使用我们的免费在线工具轻松计算点估计!
使用我们的免费在线计算器轻松计算任何百分比增加!
使用我们的数学百分比差异计算器立即计算百分比差异!
这个免费的在线计算器计算线性内插和线性外推。它还提供线性方程的斜率。
使用我们免费的在线 QR 分解计算器轻松找出正交矩阵和上三角矩阵!
此矩阵转置计算器可帮助您找到任何矩阵的转置。
使用我们的免费数学计算器轻松找出各种三角形的斜边!
使用我们的免费在线计算器轻松计算三角函数值 Sin、Cos、Tan、Cot、Sec 和 Csc!
使用我们的免费在线计算器轻松找出三角形的右侧和角度!
使用我们的 45 45 90 三角形计算器轻松计算斜边、测量值和比率。
使用我们的免费在线数学计算器轻松计算矩阵乘法!
使用我们的免费在线数学计算器轻松计算数字的平均数
该工具在任意两个数字之间生成一个真正的随机数。
此计算器根据样本大小和比例计算调查的误差幅度。它还允许您设置所需的置信度。
这个在线工具计算两个向量之间的角度,并拥有所有可能的向量组合。
这个计算器将帮助您找到一组特定数字的 LCM 或 LCD。
这个在线计算器计算以英尺为单位的形状面积。适用于所有形状和测量单位!
这是一个可以计算指数的在线计算器。
这个在线工具计算除法的余数。
使用我们免费的三法则计算器轻松计算数字的直接比例。
二次方程是在代数中具有以下形式的任何二次多项式代数。
这个求和符号计算器允许您快速计算一组数字的总和,也称为 Sigma。因此,它通常被称为 sigma 计算器。它还为您提供了该系列的样本作为总和。它可以在简单模式下使用给定的一组数字计算简单的总和。
这是一个免费的在线工具,可以计算不同形状的周长。
这是一个计算数据集 z 分数的计算器。
这个斐波那契计算器可用于任意计算斐波那契数列的项。
这是一个免费的计算器,可以帮助您找到任何胶囊的体积。
这是一个免费的计算器,可以帮助您找到不同形状的体积。
这是一个免费的计算器,可以帮助您找到任何三棱柱的体积。
这是一个免费的计算器,可以帮助您找到一个盒子的体积。
这个计算器计算圆锥体积,可用于解决学校问题。
这是一个在线工具,可以计算任何立方体的体积。
这是一个在线工具,可以计算圆柱体的体积。
这是一个在线计算器,可帮助您计算对象的比例因子膨胀。
香农生物多样性指数计算器可用于计算社区中物种的多样性。生态学家可以使用香农多样性指数来获得有关栖息地的有用信息。
使用此贝叶斯定理计算器在线确定以另一个为条件的事件的概率。该计算考虑了 A 的先验概率、B 条件概率和 A 条件概率以及 A 条件概率。
反对数计算器允许您计算反对数函数。计算任何底数的反对数,无论是 10、自然反对数还是其他数字。
这个惊人的工具将允许您计算 e 的任何您选择的数字的幂。
这个计算器会告诉你一个数是素数还是合数。
指数增长计算器根据其初始值、增长率和时间计算数量的最终价格。
根据总体规模、置信水平和误差范围计算样本量。
这个在线计算器将显示数字和输入的基数的逆对数。
泊松分布计算器将允许您确定事件在特定时间范围内多次发生的可能性。
该计算器将帮助您找到整数、小数、分数或混合数的乘法逆元。
该计算器将测试分数转换为百分比。可用于快速计算一个或多个考试成绩(分数)的百分比,以及最大分数。
当您调整图像大小时,此计算器可用于确定图像的尺寸。
经验规则计算器,也称为“68 95 99 规则计算”,是一种工具,可让您确定 1 或 2 个标准差或 3 个标准差的范围。该计算器将分别显示 68、95 或 99.7% 的正态分布数据的范围。
这个令人难以置信的工具将允许您找到 p 值。您可以使用检验统计量来确定哪个 p 值是单面的,哪个是双面的。
这是一个免费的计算器,可以帮助您找到球体的体积。
此在线计算器可让您计算投资的 NPV(净现值)。计算基于初始投资和贴现率。您还可以计算内部收益率 (IRR)、总回报和净现金流。
使用这个计算器来找出任何数量的百分比减少将如何改变结果。只需输入原始值、减少百分比和新值即可计算变化。
我们直观的工具可让您从不同的形状中进行选择,并在眨眼间计算出它们的面积。
概率计算器可让您探索两个独立事件之间的可能性关系。这使您可以更好地了解事件之间的关系,从而使预测更加准确。
使用我们的分数转小数计算器可以轻松地将分数转换为小数,然后再转换回来!
使用我们的因数计算器找出任何数字的因数
使用我们的简单工具将分数转换为带分数计算器