Αριθμομηχανή Τυπικής Απόκλισης
Αυτή η δωρεάν αριθμομηχανή σάς δίνει την τυπική απόκλιση, τη διακύμανση, τη μέση τιμή και το άθροισμα ενός δεδομένου συνόλου δεδομένων.
Πίνακας περιεχομένων
Πώς να χρησιμοποιήσετε αυτήν την αριθμομηχανή;
Τι είναι ο τύπος τυπικής απόκλισης;
Τυπική απόκλιση πληθυσμού
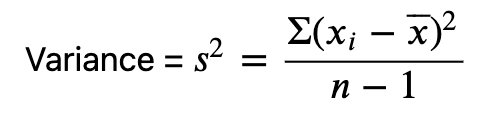

Δείγμα τυπικής απόκλισης
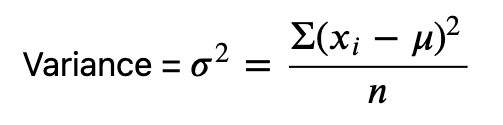
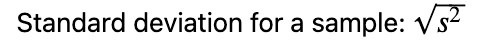
Μη διορθωμένη τυπική απόκλιση δείγματος
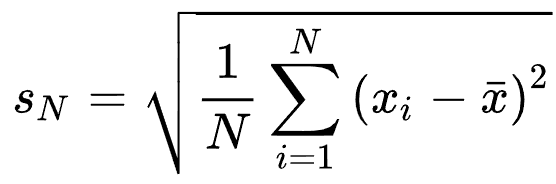
Διορθωμένη τυπική απόκλιση δείγματος
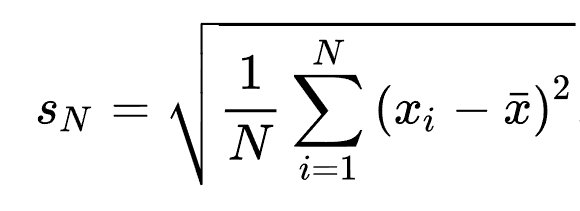
Απαρέμφατη τυπική απόκλιση δείγματος
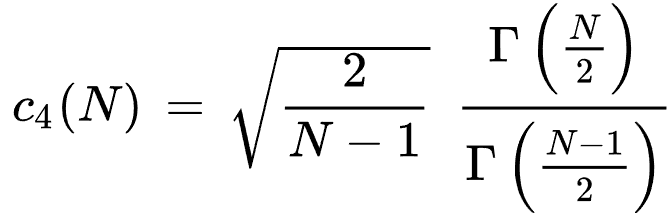
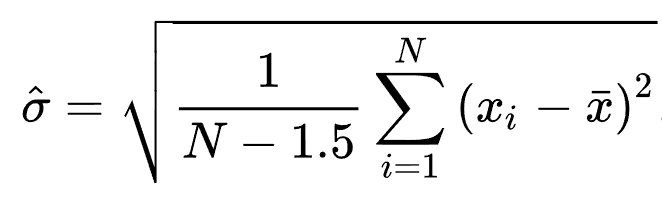
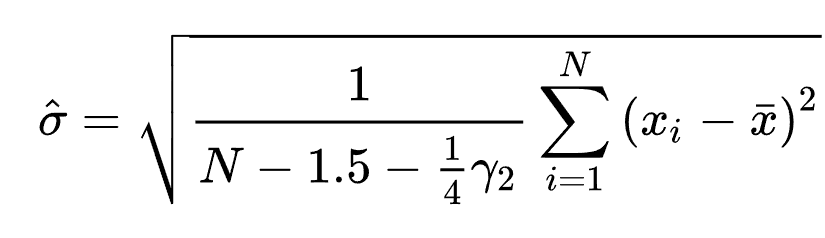
Εφαρμογές της τυπικής απόκλισης
Βιβλιογραφικές αναφορές

Αριθμομηχανή Τυπικής Απόκλισης ελληνικά
Άλλοι μαθηματικοί υπολογιστές
Ο υπολογιστής διασταυρούμενου διανύσματος βρίσκει το διασταυρούμενο προϊόν δύο διανυσμάτων σε έναν τρισδιάστατο χώρο.
Με την αριθμομηχανή τριγώνου 30 60 90 μπορείτε να λύσετε το ειδικό δεξί τρίγωνο.
Αυτός ο υπολογιστής αναμενόμενης τιμής σάς βοηθά να υπολογίσετε μια αναμενόμενη τιμή (ονομάζεται επίσης μέσος όρος) του δεδομένου συνόλου μεταβλητών με τις πιθανότητές τους.
Αυτός ο επιστημονικός υπολογιστής παρέχει απλές και προηγμένες μαθηματικές συναρτήσεις σε μια εύχρηστη εφαρμογή.
Αυτή η αριθμομηχανή ποσοστού είναι μια δωρεάν ηλεκτρονική αριθμομηχανή για τον υπολογισμό των ποσοστών. Μάθετε τι είναι το X% του Y;
Αυτός ο υπολογιστής δωρεάν κλασμάτων μπορεί να χρησιμοποιηθεί για να βρει το αποτέλεσμα για την προσθήκη, αφαίρεση, πολλαπλασιασμό και διαίρεση δύο κοινών κλασμάτων.
Μάθετε τις σωστές μετρήσεις για την αγαπημένη σας συνταγή με αυτή τη δωρεάν αριθμομηχανή που μετατρέπει εύκολα τα κιλά σε φλιτζάνια! Λειτουργεί με κύπελλα ΗΠΑ και κύπελλα Ηνωμένου Βασιλείου!
Χρησιμοποιήστε αυτόν τον δωρεάν υπολογιστή περιφέρειας κύκλου για να υπολογίσετε την ακτίνα κύκλου, τη διάμετρο του κύκλου, την περιφέρεια του κύκλου και την περιοχή του κύκλου.
Προσδιορίστε το ισοδύναμο διπλής γωνίας μιας δεδομένης γωνίας με αυτήν τη δωρεάν αριθμομηχανή! Βρείτε περισσότερες πληροφορίες σχετικά με τον τύπο διπλής γωνίας.
Αυτός ο δωρεάν υπολογιστής υπολογίζει τους δεύτερους, τρίτους και υψηλότερους εκθέτες και ρίζες. Το Formula είναι επίσης διαθέσιμο.
Μάθετε εύκολα την περιοχή του τριγώνου με τη δωρεάν αριθμομηχανή εμβαδού τριγώνου! Μπορείτε να υπολογίσετε με βάση και ύψος, τρεις διαφορετικές πλευρές και πολλές άλλες. Λειτουργεί με γωνίες και ακτίνια!
Μάθετε τις δευτερεύουσες γωνίες με τον αριθμομηχανό μας. Λειτουργεί με μοίρες και ακτίνια για να ανακαλύψετε θετικές και αρνητικές επιμήκεις γωνίες!
Υπολογίστε μαθηματικά προϊόντα κουκίδων, κλιμακωτά προϊόντα και γωνίες προϊόντων κουκίδων εύκολα για τα διανύσματά σας.
Μάθετε εύκολα τα μεσαία σημεία για μια γραμμή ή ένα τρίγωνο με την αριθμομηχανή μεσαίου σημείου! Αυτή η σελίδα θα σας διδάξει επίσης πολύτιμο τύπο μεσαίου σημείου!
Μάθετε τη σωστή ποσότητα σημαντικών αριθμών στον αριθμό σας εύκολα με το εργαλείο σημαντικών αριθμών!
Μάθετε εύκολα το μήκος του τόξου ενός κύκλου με αυτήν την ηλεκτρονική αριθμομηχανή μαθηματικών!
Υπολογίστε εύκολα την εκτίμηση πόντων με το δωρεάν διαδικτυακό μας εργαλείο!
Υπολογίστε οποιαδήποτε ποσοστιαία αύξηση εύκολα με τον δωρεάν διαδικτυακό μας υπολογιστή!
Υπολογίστε αμέσως τη διαφορά ποσοστού με τον μαθηματικό υπολογιστή ποσοστιαίας διαφοράς!
Αυτή η δωρεάν ηλεκτρονική αριθμομηχανή υπολογίζει τη γραμμική παρεμβολή και τη γραμμική επέκταση. Παρέχει επίσης την κλίση της γραμμικής εξίσωσης.
Μάθετε εύκολα την ορθόδοξη μήτρα και την ανώτερη τριγωνική μήτρα με τον δωρεάν διαδικτυακό μας αριθμομηχανή αποσύνθεσης QR!
Αυτός ο υπολογιστής μεταφοράς μήτρας σας βοηθά να βρείτε μια μεταφορά για οποιαδήποτε μήτρα.
Μάθετε εύκολα την υποτείνουσα για όλα τα είδη τριγώνων με τη δωρεάν μαθηματική αριθμομηχανή μας!
Υπολογίστε εύκολα τις τριγωνομετρικές τιμές Sin, Cos, Tan, Cot, Sec και Csc με τη δωρεάν ηλεκτρονική αριθμομηχανή μας!
Μάθετε εύκολα τη δεξιά πλευρά και τη γωνία ενός τριγώνου με τη δωρεάν ηλεκτρονική αριθμομηχανή μας!
Υπολογίστε την υποτείνουσα, τις μετρήσεις και την αναλογία εύκολα με την αριθμομηχανή τριγώνου 45 45 90.
Υπολογίστε τους πολλαπλασιασμούς πινάκων εύκολα με τη δωρεάν ηλεκτρονική μας αριθμομηχανή μαθηματικών!
Υπολογίστε εύκολα τον μέσο όρο των αριθμών με τη δωρεάν ηλεκτρονική μας αριθμομηχανή μαθηματικών
Αυτό το εργαλείο δημιουργεί έναν πραγματικά τυχαίο αριθμό μεταξύ οποιωνδήποτε δύο αριθμών.
Αυτή η αριθμομηχανή υπολογίζει το περιθώριο σφάλματος για έρευνες με βάση το μέγεθος του δείγματος και την αναλογία. Σας επιτρέπει επίσης να ορίσετε το επιθυμητό επίπεδο εμπιστοσύνης.
Αυτό το διαδικτυακό εργαλείο υπολογίζει τη γωνία μεταξύ δύο διανυσμάτων και έχει όλους τους πιθανούς συνδυασμούς διανυσμάτων.
Αυτή η αριθμομηχανή θα σας βοηθήσει να βρείτε το LCM ή την οθόνη LCD για ένα συγκεκριμένο σύνολο αριθμών.
Αυτή η ηλεκτρονική αριθμομηχανή υπολογίζει την περιοχή ενός σχήματος μετρημένη σε πόδια. Λειτουργεί με όλα τα σχήματα και τις μονάδες μέτρησης!
Αυτή είναι μια ηλεκτρονική αριθμομηχανή που μπορεί να υπολογίσει εκθέτες.
Αυτό το διαδικτυακό εργαλείο υπολογίζει το υπόλοιπο μιας διαίρεσης.
Υπολογίστε εύκολα την άμεση αναλογία αριθμών με τη δωρεάν αριθμομηχανή Κανόνας των Τριών.
Τετραγωνικές εξισώσεις είναι οποιαδήποτε πολυωνυμική άλγεβρα δεύτερου βαθμού που έχει την ακόλουθη μορφή στην άλγεβρα.
Αυτός ο υπολογιστής σημειογραφίας αθροίσματος σάς επιτρέπει να υπολογίζετε γρήγορα το άθροισμα ενός συνόλου αριθμού, γνωστό και ως Sigma. Ως εκ τούτου, συχνά ονομάζεται αριθμομηχανή σίγμα. Σου δίνει και δείγμα από τη σειρά για να είναι άθροισμα. Μπορεί να χρησιμοποιηθεί σε απλή λειτουργία για τον υπολογισμό ενός απλού αθροίσματος χρησιμοποιώντας ένα δεδομένο σύνολο αριθμών.
Αυτό είναι ένα δωρεάν διαδικτυακό εργαλείο που θα υπολογίσει την περίμετρο διαφορετικών σχημάτων.
Αυτή είναι μια αριθμομηχανή που υπολογίζει το z-score ενός συνόλου δεδομένων.
Αυτή η αριθμομηχανή Fibonacci μπορεί να χρησιμοποιηθεί για τον αυθαίρετο υπολογισμό των όρων της ακολουθίας Fibonacci.
Είναι μια δωρεάν αριθμομηχανή που μπορεί να σας βοηθήσει να βρείτε τον όγκο οποιασδήποτε κάψουλας.
Είναι μια δωρεάν αριθμομηχανή που μπορεί να σας βοηθήσει να βρείτε τον όγκο διαφορετικών σχημάτων.
Είναι μια δωρεάν αριθμομηχανή που μπορεί να σας βοηθήσει να βρείτε τον όγκο οποιουδήποτε τριγωνικού πρίσματος.
Είναι μια δωρεάν αριθμομηχανή που μπορεί να σας βοηθήσει να βρείτε τον όγκο ενός κουτιού.
Αυτή η αριθμομηχανή υπολογίζει τον όγκο του κώνου και μπορεί να χρησιμοποιηθεί για την επίλυση σχολικών προβλημάτων.
Αυτό είναι ένα διαδικτυακό εργαλείο που θα υπολογίσει τον όγκο οποιουδήποτε κύβου.
Αυτό είναι ένα διαδικτυακό εργαλείο που θα υπολογίσει τον όγκο ενός κυλίνδρου.
Αυτή είναι μια ηλεκτρονική αριθμομηχανή που θα σας βοηθήσει να υπολογίσετε τη διαστολή του παράγοντα κλίμακας ενός αντικειμένου.
Ο υπολογιστής δείκτη βιοποικιλότητας Shannon μπορεί να χρησιμοποιηθεί για τον υπολογισμό της ποικιλότητας των ειδών σε μια κοινότητα. Οι οικολόγοι μπορούν να χρησιμοποιήσουν τον δείκτη ποικιλότητας Shannon για να αποκτήσουν χρήσιμες πληροφορίες σχετικά με τον βιότοπο.
Χρησιμοποιήστε αυτόν τον υπολογιστή του θεωρήματος Bayes online για να προσδιορίσετε την πιθανότητα ενός γεγονότος που εξαρτάται από ένα άλλο. Αυτός ο υπολογισμός λαμβάνει υπόψη την προηγούμενη πιθανότητα του Α, τις πιθανότητες Β υπό όρους και Α υπό όρους και Α υπό όρους.
Η αριθμομηχανή antilog σάς επιτρέπει να υπολογίσετε τη συνάρτηση αντίστροφου λογάριθμου. Υπολογίστε τον αντιλογάριθμο για οποιονδήποτε αριθμό με οποιαδήποτε βάση, είτε είναι 10, φυσικό αντίλογο ή άλλος αριθμός.
Αυτό το εκπληκτικό εργαλείο θα σας επιτρέψει να υπολογίσετε το e στην ισχύ οποιουδήποτε αριθμού επιλέξετε.
Αυτή η αριθμομηχανή θα σας δείξει εάν ένας αριθμός έχει πρώτο αριθμό ή εάν είναι σύνθετος.
Ο Υπολογιστής εκθετικής ανάπτυξης υπολογίζει την τελική τιμή μιας ποσότητας με βάση τις αρχικές τιμές, το ρυθμό ανάπτυξης και το χρόνο της.
Υπολογίστε το μέγεθος του δείγματος με βάση το μέγεθος του πληθυσμού, το επίπεδο εμπιστοσύνης και το περιθώριο σφάλματος.
Αυτή η ηλεκτρονική αριθμομηχανή θα εμφανίσει το αντίστροφο αρχείο καταγραφής του αριθμού και της βάσης που εισάγατε.
Ο υπολογιστής κατανομής Poisson θα σας επιτρέψει να προσδιορίσετε την πιθανότητα να συμβεί ένα συμβάν πολλές φορές κατά τη διάρκεια ενός συγκεκριμένου χρονικού πλαισίου.
Αυτή η αριθμομηχανή θα σας βοηθήσει να βρείτε το πολλαπλασιαστικό αντίστροφο ενός ακέραιου, ενός δεκαδικού, ενός κλάσματος ή ενός μικτού αριθμού.
Αυτή η αριθμομηχανή μετατρέπει τα σημάδια δοκιμής σε ποσοστά. Μπορεί να χρησιμοποιηθεί για τον γρήγορο υπολογισμό του ποσοστού ενός ή περισσότερων βαθμών δοκιμής (βαθμών) και του μέγιστου αριθμού βαθμών.
Αυτή η αριθμομηχανή μπορεί να χρησιμοποιηθεί για τον προσδιορισμό των διαστάσεων των εικόνων όταν αλλάζετε το μέγεθός τους.
Ο εμπειρικός υπολογιστής κανόνων, γνωστός και ως "υπολογισμός κανόνων 68 95 99", είναι ένα εργαλείο που σας επιτρέπει να προσδιορίσετε τις περιοχές που είναι είτε 1 είτε 2 τυπικές αποκλίσεις είτε 3 τυπικές αποκλίσεις. Αυτή η αριθμομηχανή θα σας δείξει τις περιοχές στις οποίες είναι 68, 95 ή 99,7% των κανονικά κατανεμημένων δεδομένων, αντίστοιχα.
Αυτό το απίστευτο εργαλείο θα σας επιτρέψει να βρείτε την τιμή p. Μπορείτε να χρησιμοποιήσετε στατιστικά στοιχεία δοκιμής για να προσδιορίσετε ποια τιμή p είναι μονόπλευρη και ποια διπλής όψης.
Είναι μια δωρεάν αριθμομηχανή που μπορεί να σας βοηθήσει να βρείτε τον όγκο μιας σφαίρας.
Αυτή η ηλεκτρονική αριθμομηχανή θα σας επιτρέψει να υπολογίσετε το NPV (Καθαρή Παρούσα Αξία) μιας επένδυσης. Ο υπολογισμός βασίζεται στην αρχική επένδυση και στο προεξοφλητικό επιτόκιο. Μπορείτε επίσης να υπολογίσετε τα εσωτερικά ποσοστά απόδοσης (IRR), τις μικτές αποδόσεις και τις καθαρές ταμειακές ροές.
Χρησιμοποιήστε αυτήν την αριθμομηχανή για να μάθετε πώς μια ποσοστιαία μείωση κατά οποιοδήποτε ποσό θα αλλάξει το αποτέλεσμα. Απλώς εισαγάγετε την αρχική τιμή, την ποσοστιαία μείωση και τη νέα τιμή για να υπολογίσετε την αλλαγή.
Το διαισθητικό εργαλείο μας σάς επιτρέπει να επιλέξετε από διαφορετικά σχήματα και να υπολογίζει την περιοχή τους εν ριπή οφθαλμού.
Ο υπολογιστής πιθανοτήτων σάς επιτρέπει να εξερευνήσετε τις σχέσεις πιθανότητας μεταξύ δύο ξεχωριστών γεγονότων. Αυτό σας επιτρέπει να κατανοήσετε καλύτερα τον τρόπο με τον οποίο σχετίζονται τα γεγονότα και, ως εκ τούτου, καθιστά τις προβλέψεις πιο ακριβείς.
Χρησιμοποιήστε την αριθμομηχανή κλάσματος σε δεκαδικό για να μετατρέψετε εύκολα τα κλάσματα σε δεκαδικά και πάλι πίσω!
Μάθετε τους συντελεστές οποιουδήποτε αριθμού με την αριθμομηχανή συντελεστών μας
Μετατρέψτε ένα κλάσμα σε έναν μικτό αριθμομηχανή χρησιμοποιώντας το απλό μας εργαλείο