목차
| ◦이 계산기를 사용하는 방법? |
| ◦표준편차 공식이란? |
| ◦모집단 표준편차 |
| ◦표본 표준편차 |
| ◦수정되지 않은 표본 표준 편차 |
| ◦수정된 표본 표준 편차 |
| ◦편향되지 않은 표본 표준 편차 |
| ◦표준편차의 적용 |
| ◦참고문헌 |
이 계산기를 사용하는 방법?
표준편차 공식이란?
모집단 표준편차
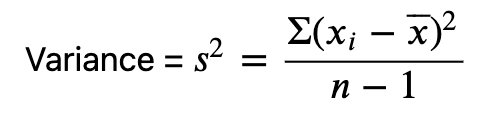

표본 표준편차
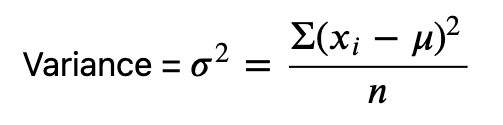
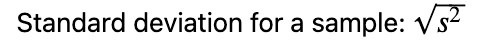
수정되지 않은 표본 표준 편차
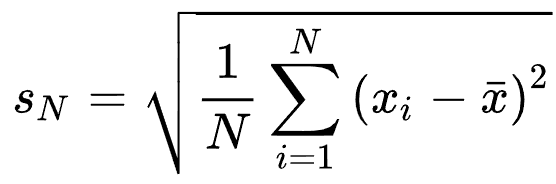
수정된 표본 표준 편차
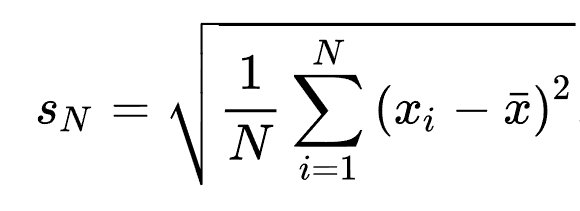
편향되지 않은 표본 표준 편차
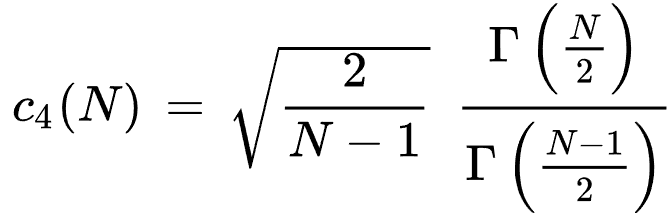
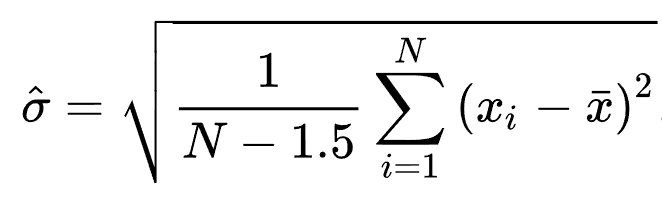
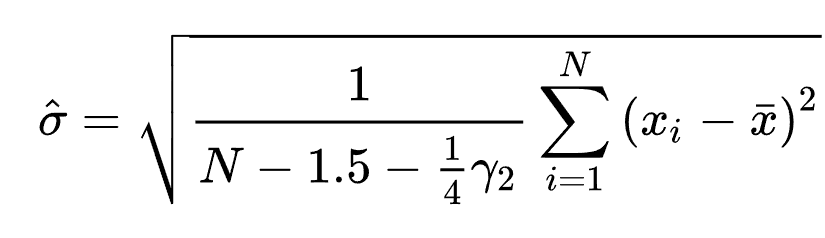
표준편차의 적용
참고문헌

표준편차 계산기 한국어
기타 수학 계산기
벡터 외적 계산기는 3차원 공간에서 두 벡터의 외적을 찾습니다.
30 60 90 삼각형 계산기를 사용하면 특별한 직각 삼각형을 풀 수 있습니다.
이 기대값 계산기는 확률과 함께 주어진 변수 세트의 기대값(평균이라고도 함)을 계산하는 데 도움이 됩니다.
이 공학용 계산기는 사용하기 쉬운 앱에서 간단하고 고급 수학 기능을 제공합니다.
이 백분율 계산기는 백분율을 계산하는 무료 온라인 계산기입니다. Y의 X %가 무엇인지 알아내십시오.
이 무료 분수 계산기는 두 개의 공통 분수 더하기, 빼기, 곱하기 및 나누기에 대한 결과를 찾는 데 사용할 수 있습니다.
파운드를 컵으로 쉽게 변환하는 이 무료 계산기를 사용하여 좋아하는 레시피에 대한 정확한 측정값을 찾으십시오! 미국 컵 및 영국 컵과 함께 작동합니다!
이 무료 원 둘레 계산기를 사용하여 원 반지름, 원 지름, 원 원주 및 원 면적을 계산하십시오.
이 무료 계산기로 주어진 각도에 해당하는 이중 각도를 결정하십시오! 이중 각 공식에 대한 자세한 정보를 찾으십시오.
이 무료 계산기는 두 번째, 세 번째 및 더 높은 지수와 근을 계산합니다. 공식도 가능합니다.
무료 삼각형 면적 계산기로 삼각형의 면적을 쉽게 알아보세요! 밑변과 높이, 3개의 다른 면 등을 사용하여 계산할 수 있습니다. 각도와 라디안으로 작동합니다!
우리의 동일 끝 각도 계산기로 동일 끝 각도를 찾으십시오! 도 및 라디안과 함께 작동하여 양수 및 음수 공동 터미널 각도를 찾습니다!
벡터에 대한 수학적 내적, 스칼라 곱 및 내적 각도를 쉽게 계산합니다.
중간점 계산기를 사용하여 선 또는 삼각형의 중간점을 쉽게 찾으십시오! 이 페이지는 또한 중요한 중간점 공식을 알려줄 것입니다!
유효 숫자 도구를 사용하여 숫자에서 유효 숫자의 정확한 양을 쉽게 알아보세요!
이 온라인 수학 계산기로 원호의 길이를 쉽게 알아보세요!
무료 온라인 도구를 사용하여 예상 포인트를 쉽게 계산하십시오!
무료 온라인 계산기로 백분율 증가를 쉽게 계산하십시오!
수학적 백분율 차이 계산기로 백분율 차이를 즉시 계산하십시오!
이 무료 온라인 계산기는 선형 보간과 선형 외삽을 계산합니다. 또한 선형 방정식의 기울기를 제공합니다.
무료 온라인 QR 분해 계산기를 사용하여 직교 행렬과 상부 삼각 행렬을 쉽게 찾으십시오!
이 행렬 전치 계산기는 모든 행렬에 대한 전치를 찾는 데 도움이 됩니다.
무료 수학 계산기로 모든 종류의 삼각형에 대한 빗변을 쉽게 찾아보세요!
무료 온라인 계산기를 사용하여 삼각법 값 Sin, Cos, Tan, Cot, Sec 및 Csc를 쉽게 계산하십시오!
무료 온라인 계산기로 삼각형의 직각과 각도를 쉽게 알아보세요!
45 45 90 삼각형 계산기로 빗변, 치수 및 비율을 쉽게 계산하십시오.
무료 온라인 수학 계산기로 행렬 곱셈을 쉽게 계산하십시오!
무료 온라인 수학 계산기를 사용하여 숫자의 평균 평균을 쉽게 계산하십시오.
이 도구는 두 숫자 사이에 진정한 난수를 생성합니다.
이 계산기는 표본 크기와 비율에 따라 설문조사의 오차 한계를 계산합니다. 또한 원하는 신뢰도 수준을 설정할 수 있습니다.
이 온라인 도구는 두 벡터 사이의 각도를 계산하고 가능한 모든 벡터 조합을 가지고 있습니다.
이 계산기는 특정 숫자 집합에 대한 LCM 또는 LCD를 찾는 데 도움이 됩니다.
이 온라인 계산기는 피트로 측정된 모양의 면적을 계산합니다. 모든 모양 및 측정 단위와 함께 작동합니다!
지수를 계산할 수 있는 온라인 계산기입니다.
이 온라인 도구는 나눗셈의 나머지를 계산합니다.
무료 3법칙 계산기를 사용하여 숫자의 직접 비율을 쉽게 계산하십시오.
이차 방정식은 대수에서 다음 형식을 갖는 2차 다항식 대수입니다.
이 합산 표기법 계산기를 사용하면 시그마라고도 하는 집합 수의 합을 빠르게 계산할 수 있습니다. 따라서 종종 시그마 계산기라고 합니다. 또한 시리즈의 샘플을 합계로 제공합니다. 단순 모드에서 주어진 숫자 세트를 사용하여 단순 합계를 계산하는 데 사용할 수 있습니다.
이것은 다양한 모양의 둘레를 계산하는 무료 온라인 도구입니다.
이것은 데이터 세트의 z-점수를 계산하는 계산기입니다.
이 피보나치 계산기는 피보나치 수열의 항을 임의로 계산하는 데 사용할 수 있습니다.
모든 캡슐의 부피를 찾는 데 도움이 되는 무료 계산기입니다.
다양한 모양의 부피를 찾는 데 도움이 되는 무료 계산기입니다.
삼각형 프리즘의 부피를 찾는 데 도움이 되는 무료 계산기입니다.
상자의 부피를 찾는 데 도움이 되는 무료 계산기입니다.
이 계산기는 원뿔 부피를 계산하고 학교 문제를 해결하는 데 사용할 수 있습니다.
이것은 모든 큐브의 부피를 계산하는 온라인 도구입니다.
이것은 실린더의 부피를 계산하는 온라인 도구입니다.
이것은 물체의 축척 계수 팽창을 계산하는 데 도움이 되는 온라인 계산기입니다.
Shannon 생물다양성 지수 계산기는 지역 사회의 종의 다양성을 계산하는 데 사용할 수 있습니다. 생태학자는 Shannon 다양성 지수를 사용하여 서식지에 대한 유용한 정보를 얻을 수 있습니다.
이 베이즈 정리 계산기를 온라인으로 사용하여 다른 이벤트에 대한 조건부 이벤트의 확률을 결정하십시오. 이 계산은 A의 사전 확률, 조건 B 및 A 조건, A 조건을 고려합니다.
안티로그 계산기를 사용하면 역 로그 함수를 계산할 수 있습니다. 10이든, 자연적 역수이든, 다른 숫자이든 상관없이 모든 밑수를 사용하여 숫자에 대한 역대수를 계산합니다.
이 놀라운 도구를 사용하면 선택한 숫자의 거듭제곱으로 e를 계산할 수 있습니다.
이 계산기는 숫자에 소수가 있는지 또는 합성인지 여부를 보여줍니다.
지수 성장 계산기는 초기 값, 성장률 및 시간을 기반으로 수량의 최종 가격을 계산합니다.
모집단 크기, 신뢰 수준 및 오차 한계를 기반으로 표본 크기를 계산합니다.
이 온라인 계산기는 입력된 숫자와 밑수의 역 로그를 표시합니다.
포아송 분포 계산기를 사용하면 특정 시간 프레임 동안 여러 번 발생하는 이벤트의 가능성을 결정할 수 있습니다.
이 계산기는 정수, 소수, 분수 또는 대분수의 곱셈의 역수를 찾는 데 도움이 됩니다.
이 계산기는 테스트 점수를 백분율로 변환합니다. 하나 이상의 시험 성적(점수)의 백분율과 최대 점수를 빠르게 계산하는 데 사용할 수 있습니다.
이 계산기는 이미지 크기를 조정할 때 이미지의 크기를 결정하는 데 사용할 수 있습니다.
"68 95 99 규칙 계산"이라고도 하는 경험적 규칙 계산기는 1 또는 2 표준 편차 또는 3 표준 편차인 범위를 결정할 수 있는 도구입니다. 이 계산기는 각각 정규 분포 데이터의 68, 95 또는 99.7% 범위를 보여줍니다.
이 놀라운 도구를 사용하면 p-값을 찾을 수 있습니다. 검정 통계량을 사용하여 단측 p-값과 양측 p-값을 확인할 수 있습니다.
구의 부피를 구하는 데 도움이 되는 무료 계산기입니다.
이 온라인 계산기를 사용하면 투자의 NPV(순 현재 가치)를 계산할 수 있습니다. 계산은 초기 투자 및 할인율을 기반으로 합니다. 내부 수익률(IRR), 총 수익률 및 순 현금 흐름을 계산할 수도 있습니다.
이 계산기를 사용하여 백분율 감소가 결과를 어떻게 변경하는지 알아보세요. 원래 값, 감소 비율 및 새 값을 입력하여 변경 사항을 계산하기만 하면 됩니다.
직관적인 도구를 사용하면 다양한 모양 중에서 선택하고 눈 깜짝할 사이에 면적을 계산할 수 있습니다.
확률 계산기를 사용하면 두 개의 개별 이벤트 간의 가능성 관계를 탐색할 수 있습니다. 이를 통해 이벤트가 어떻게 관련되어 있는지 더 잘 이해할 수 있으므로 예측이 더 정확해집니다.
분수를 소수로 쉽게 변환하고 다시 소수로 변환하려면 분수-소수 계산기를 사용하세요!
인수 계산기로 숫자의 인수를 찾으십시오.
간단한 도구를 사용하여 분수를 대분수 계산기로 변환